Диэлектриков

Граничные условия на поверхности раздела двух

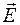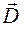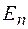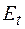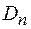Вблизи поверхности раздела двух диэлектриков векторы и должны удовлетворять определенным граничным условиям. Установим, каким образом изменяются при переходе через границу двух сред значения нормальных и тангенциальных компонент этих векторов: и , и .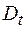

Рассмотрим границу двух однородных и изотропных диэлектриков с диэлектрическими проницаемостям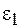и и .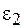

Изобразим небольшой прямоугольный контур L длиной а и шириной b, который частично находится в первом диэлектрике, частично во втором (рис. 48.1). Чтобы исследовать изменение характеристик поля на границе диэлектриков, длинные стороны контура должны располагаться у поверхности раздела, т. е. .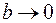

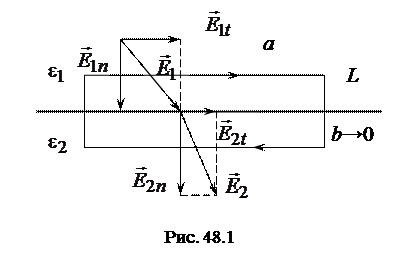Пусть в диэлектриках создано электрическое поле, напряженность которого в первом из них , а во втором . Найдем циркуляцию вектора напряженности по контуру L:

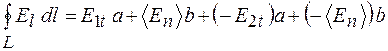, (48.1)

где 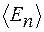- среднее значение на перпендикулярных к границе участках контура.

Так как циркуляция вектора напряженности равна нулю 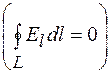и , то из формулы (48.1) находим

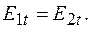(48.2)

Учитывая соотношение 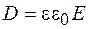, на основании формулы (48.2) для тангенциальных составляющих вектора электрического смещения получаем

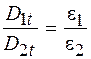. (48.3)

Теперь рассмотрим на границе диэлектриков воображаемую цилиндрическую поверхность высотой 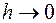(рис. 48.2). Основание

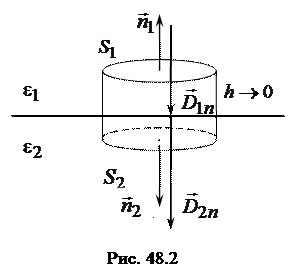расположено в первом диэлектрике, основание – во втором. При этом и они настолько малы, что в пределах каждого из них поле можно считать однородным.

Найдем поток вектора через выделенную цилиндрическую поверхность:

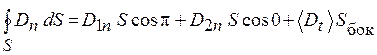, (48.4)

где 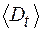- среднее значение 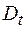в пределах всей боковой поверхности 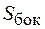цилиндра. Поскольку 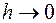, то 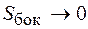. Поэтому соотношение (48.4) принимает вид

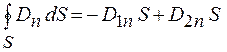. (48.5)

По теореме Гаусса 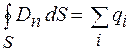, но так как свободных зарядов на границе диэлектриков нет, то 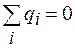и 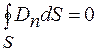. Тогда из формулы (48.5) находим

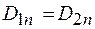. (48.6)

Подставив в формулу (48.6) 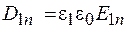, , 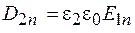получим для нормальных компонент напряженности

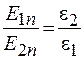. (48.7)

На основании формул (48.2), (48.3), (48.6) и (48.7) делаем следующий вывод. При переходе через границу раздела двух диэлектриков нормальная составляющая вектора смещения 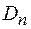и тангенциальная составляющая вектора напряженности 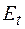не изменяются; тангенциальная составляющая вектора смещения 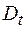и нормальная составляющая вектора напряженности 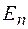изменяются скачком.

Эти соотношения справедливы и для полей, изменяющихся со временем. Следует учитывать, что все рассуждения велись при условии отсутствия на границе диэлектриков свободных электрических зарядов. Найденные условия справедливы и для границы диэлектрика с вакуумом. В этом случае одно из значений диэлектрической проницаемости нужно принять равным единице. Если одной из сред является металл, то соответствующее значение диэлектрической проницаемости принимается равным бесконечности.

На границе диэлектриков линии вектора 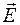терпят излом (преломляются), вследствие чего угол a между перпендикуляром к поверхности раздела диэлектриков и линией напряженности изменяется (рис. 48.3).

Из рисунка следует, что

.

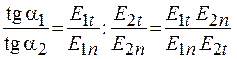Так как 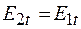, то получаем

.

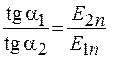Учитывая соотношение (48.7), эту формулу преобразуем к виду

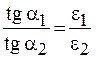. (48.8)

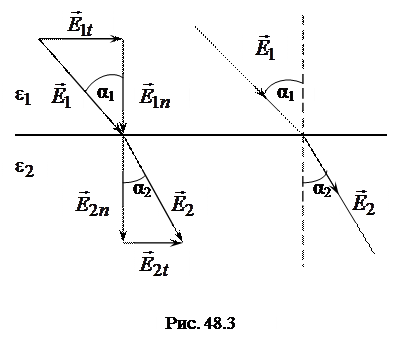
Из формулы (48.8) следует, что в среде с большей диэлектрической проницаемостью линии напряженности составляют больший угол с перпендикуляром к границе раздела.

Дата добавления: 2014-01-05