Металлов

Основы классической теории электропроводности

Формах

Закон Ома в интегральной и дифференциальной

Г. С. Ом в 1826 г. установил, что сила тока на однородном участке цепи прямо пропорциональна напряжению U (разности потенциалов) на концах проводника:

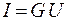, (54.1)

где G - электрическая проводимость. Она зависит от материала, формы и размеров проводника, его температуры.

Величина, обратная электрической проводимости

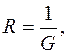
называется электрическим сопротивлением (для краткости - сопротивлением) проводника.

Сопротивление также зависит от температуры, формы, размеров проводника и свойств материала, из которого он изготовлен. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется формулой

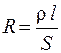. (54.2)

Входящая в нее величина r называется удельным сопротивлением и также зависит от материала и температуры. У металлов при нагревании удельное сопротивление увеличивается по линейному закону:

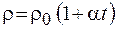r, (54.3)

где 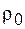- удельное сопротивление при 0 °C, 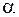- температурный коэффициент сопротивления, t - температура по шкале Цельсия.

Объединяя формулы (54.1) и (54.2) находим

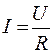. (54.4)

Выражения (54.1) и (54.4) называют законом Ома для однородного участка цепи, или законом Ома в интегральной форме.

Подставим выражение (54.2) в уравнение (54.4) и выполним преобразования:

,

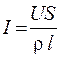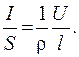(54.5)

Производим замену:

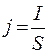- плотность тока,

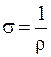- удельная проводимость вещества,

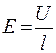– напряженность электрического поля в проводнике.

В итоге уравнение (54.5) приводим к виду

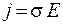. (54.6)

Формула (54.6) описывает закон Ома в дифференциальной форме: плотность тока прямо пропорциональна напряженности электрического поля в проводнике.

В каждой точке проводника 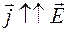, поэтому выражение (54.6) можем записать в векторной форме:

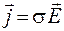. (54.7)

Единица электрической проводимости - сименс (См), единица сопротивления - ом (1 Ом =1 См^-1), удельного сопротивления - ом-метр (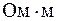). Поскольку удельная проводимость 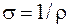, то ее единица - сименс на метр (См/м).

В металлах ток создается движением свободных электронов. Они образуются вследствие того, что при образовании кристалла из атомов их валентные электроны приобретают способность перемещаться по всему кристаллу. В отсутствие поля электроны движутся хаотически, участвуя в тепловом движении подобно молекулам газа, поэтому совокупность свободных электронов называется электронным газом. Скорость и энергия хаотичного теплового движения электронов зависят от температуры металла. При создании электрического поля на беспорядочное движение электронов накладывается упорядоченное движение. Такое движение называется дрейфом. Дрейф электронов обеспечивает перенос электрического заряда по цепи, т. е. электрический ток.

Теория проводимости металлов, построенная на этих представлениях, называется классической электронной теорией проводимости. Она была разработана П. Друде, а затем усовершенствована Х. Лоренцем.

Если среднюю скорость упорядоченного движения электронов обозначить 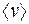, а их концентрацию 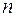, то заряд, перенесенный за время dt через поперечное сечение проводника S, будет равен

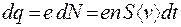. (55.1)

Используя уравнения (55.1), (53.2) и (53.4), получим выражения для силы и плотности тока:

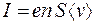, (55.2)

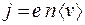. (55.3)

Учитывая, что вектор 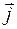направлен противоположно скорости дрейфа электронов 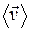и заряд их 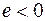, формулу (55.3) можно записать в векторной форме:

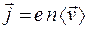. (55.4)

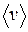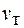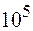Полученные выражения позволяют оценить скорость направленного движения электронов в проводнике. В металлах ее значение ~ м/с, в то время как тепловое движение характеризуется ~ м/с.

В теории Друде–Лоренца предполагается, что электроны проводимости в промежутках между соударениями движутся совершенно свободно, пробегая в среднем расстояние 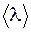. В отличие от молекул газа, пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. При включении электрического поля на хаотическое тепловое движение накладывается упорядоченное движение (дрейф) электронов с некоторой средней скоростью 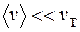. Поэтому при вычислениях значение результирующей скорости можно заменить скоростью теплового движения .

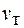На основании классической теории проводимости металла могут быть получены математические выражения законов Ома и Джоуля–Ленца. Покажем это на примере закона Ома в дифференциальной форме.

Друде считал, что при соударении электрона с ионом кристаллической решетки приобретенная электроном дополнительная энергия полностью передается иону и, следовательно, скорость электрона в результате соударения становится равной нулю. Со стороны электрического поля на электрон действует сила 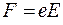, сообщающая ему ускорение

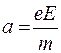. (55.5)

К концу свободного пробега электрон приобретает скорость

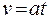, (55.6)

где t - время между двумя последовательными соударениями электрона с ионами кристаллической решетки.

Так как между соударениями электрон проходит расстояние, равное средней длине свободного пробега 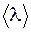, двигаясь со скоростью 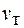, то

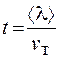. (55.7)

Объединяя выражения (55.5), (55.6) и (55.7), получаем

.

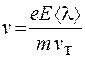Учитывая, что движение электрона начинается со скоростью 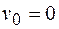, для средней скорости получаем 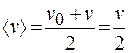. В соответствии с этим находим

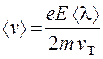. (55.8)

Из формулы (55.8) видно, что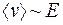. Следовательно, отношение этих величин будет постоянной для данного проводника величиной:

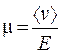. (55.9)

Физическая величина, равная отношению средней скорости направленного движения (дрейфа) свободных носителей заряда к напряженности электрического поля, называется подвижностью.

Единица подвижности - метр в квадрате на вольт-секунду .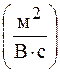

Используем выражения (55.3) и (55.8) для нахождения плотности электрического тока:

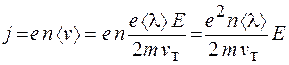. (55.10)

Сопоставив формулы (55.10) и (54.6) делаем вывод, что выражение (55.10) представляет собой закон Ома в дифференциальной форме:

,

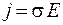где удельная проводимость определяется выражением

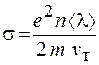. (55.11)

Учитывая, что r = 1/s, из формулы (55.11) получаем выражение для удельного сопротивления:

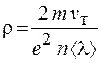. (55.12)

У металлов значения концентрации n и средней длины свободного пробега электронов 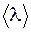практически не зависят от температуры. Скорость теплового движения 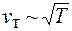. Тогда на основании формулы (55.12) заключаем, что 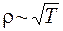. Вывод этот противоречит опытным данным, согласно которым r ~ Т. Это затруднение классической теории находит объяснение лишь в квантовой теории проводимости металлов.

Дата добавления: 2014-01-05