И его решение. Дифференциальное уравнение гармонических колебаний

Дифференциальное уравнение гармонических колебаний

Рассмотренные в предыдущем параграфе примеры показывают, что колебательные системы, несмотря на различия в конструкции и даже физической природе процессов, происходящих в них, описываются одним и тем же уравнением вида

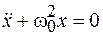, (3.1)

где 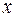– некоторая физическая величина, характеризующая состояние системы; 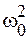– постоянная величина, зависящая от параметров системы. Это уравнение называется дифференциальным уравнением гармонических колебаний.

Уравнение (3.1) представляет собой линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение можно представить в виде

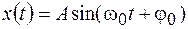. (3.2)

Используя формулы приведения, решение (3.2) можно записать в виде

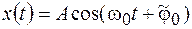, (3.3)

где .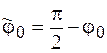

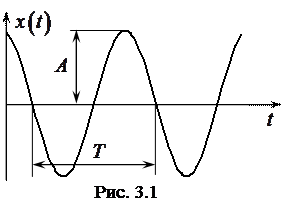Колебания, имеющие синусоидальную или косинусоидальную форму, называются гармоническими, а сама колебательная система, в которой происходят гармонические колебания – гармоническим осциллятором. Таким образом, уравнение вида (3.1) представляет собой дифференциальное уравнение гармонических колебаний, а его решения (3.2), (3.3) описывают гармонические колебания. График гармонического колебания изображен на рисунке 3.1.

Максимальное отклонение А физической величины 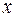, характеризующей состояние колебательной системы, от равновесного состояния называется амплитудой колебания. Величина 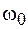в выражениях (3.2), (3.3) называется циклической частотой колебаний. Циклическая частота равна числу колебаний, совершаемых за время 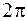секунд. Число колебаний, совершаемых в единицу времени, называется частотой колебаний 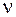. Частота 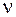связана с циклической частотой 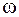соотношением

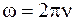. (3.4)

Наименьший интервал времени 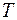, по истечении которого колебательная система возвращается в первоначальное состояние, называется периодом колебаний. Частота колебаний 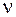и циклическая частота 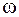связаны с периодом 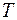соотношениями

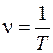; (3.5)

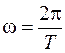. (3.6)

Величина 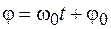в выражениях (3.2), (3.3) называется фазой колебаний. Фаза колебаний 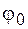в начальный момент времени 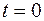называется начальной фазой колебаний.

Размерность амплитуды колебаний А определяется размерностью физической величины 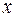, характеризующей состояние колебательной системы. Период колебаний, как это следует из определения, измеряется в секундах. Частота n измеряется в герцах. Один герц соответствует одному колебанию в секунду (1 Гц 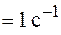). Размерность циклической частоты: 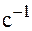или рад/с. Фаза колебаний измеряется в радианах.

Рассмотренные примеры показывают, что если состояние колебательной системы описывается дифференциальным уравнением вида (3.1), то в такой системе могут происходить свободные (собственные) гармонические колебания вида (3.2), (3.3), причем коэффициент 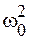в уравнении (3.1) представляет собой квадрат циклической частоты колебаний. Циклическая частота (а значит и период колебаний) определяется только параметрами колебательной системы и не зависит от амплитуды и фазы колебаний (табл. 3.1).

Таблица 3.1

Колебательная система	Математи-ческий маятник	Физический маятник	Пружинный маятник	LC -контур
Период колебаний Т, с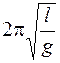

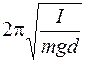
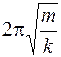
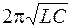
Гармонические колебания возникают при условии, когда отклонение системы от положения равновесия вызывает действие "возвращающей силы" (любой природы), направленной к положению равновесия и прямо пропорциональной отклонению от положения равновесия.

Амплитуда и начальная фаза колебаний определяются начальными условиями, под которыми понимаются значения искомой функции 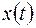и ее первой производной 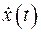в начальный момент времени (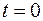), т. е. 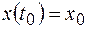и 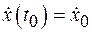. Если начальные условия известны, то, приравнивая 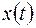и ее производную в момент времени 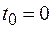заданным значениям, получим систему уравнений

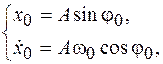
решая которую, получим

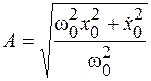, (3.7)

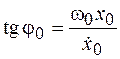. (3.8)

§ 4. Энергетические превращения,

Дата добавления: 2014-01-05