Дифференциальное уравнение затухающих колебаний

В реальных колебательных системах всегда имеются потери энергии колебаний. В механических системах потери обусловлены чаще всего трением. В электрических колебательных системах происходит выделение джоулева тепла на активном сопротивлении, что приводит к уменьшению энергии колебаний. Электрические колебания сопровождаются излучением электромагнитных волн, которые уносят часть энергии колебательной системы (потери на излучение). Независимо от физической природы потери энергии приводят к тому, что амплитуда колебаний с течением времени уменьшается, поэтому колебания называются затухающими. Рассмотрим колебания гармонического осциллятора с учетом потерь:

а) пружинный маятник

Пусть на груз (рис. 2.3) кроме упругой силы деформированной пружины действует сила сопротивления среды, в которой происходят колебания. При малых скоростях движения груза эта сила прямо пропорциональна скорости, т. 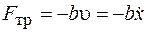е. , где 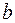– коэффициент пропорциональности.

Тогда в правой части уравнения (2.4) следует добавить силу сопротивления и это уравнение примет вид

.

Разделив обе части уравнения на 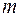, приведем его к виду

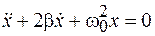, (9.1)

где обозначено и ;

б) - контур

Пусть в контуре кроме конденсатора и катушки индуктивности имеется активное сопротивление 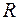(рис. 9.1). Составляя для такого контура уравнение по второму закону Кирхгофа, как это делалось в § 2, необходимо учесть падение напряжения на активном сопротивлении, которое в соответствии с законом Ома 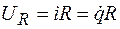. Тогда это уравнение запишется следующим образом:

.

Разделив обе части уравнения на 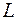, приведем его к виду

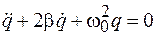, (9.2)

где введены обозначения и .

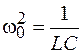Уравнения (9.1) и (9.2) совпадают с точностью до обозначений, поэтому уравнение вида

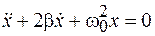(9.3)

называется дифференциальным уравнением свободных затухающих колебаний. Коэффициент 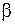называется коэффициентом затухания и, как видно из рассмотренных примеров, он определяется параметрами колебательной системы. Коэффициент затухания измеряется в .

Дата добавления: 2014-01-05