Вынужденные колебания в электрических цепях

При последовательном включении ЭДС в -контур заряд на обкладках конденсатора будет изменяться по гармоническому закону с частотой внешней ЭДС:

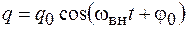. (15.1)

С учетом того, что 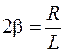, 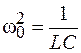и 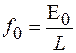, для амплитуды заряда 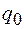из (12.9) после простых алгебраических преобразований получим

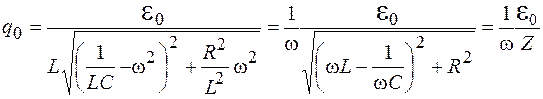, (15.2)

где 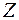– импеданс цепи. По закону Ома – амплитуда силы тока в контуре и тогда можно записать 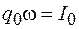. Из (12.14) находим, что сдвиг фазы 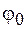между колебаниями заряда на обкладках конденсатора и внешней ЭДС определяется выражением

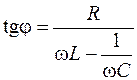, (15.3)

т. е., как и ранее, определяется отношением активного и реактивного сопротивлений цепи. Резонансная частота при этом

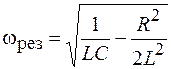. (15.4)

При малых потерях в контуре можно считать, что резонансная частота совпадает с частотой собственных колебаний, т. е.

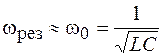. (15.5)

На резонансной частоте при малых потерях в контуре емкостное и индуктивное сопротивления равны друг другу по величине, а полное сопротивление цепи минимально и равно активному сопротивлению: . Таким образом, на резонансной частоте колебательный контур ведет себя как активное сопротивление. При этом катушка индуктивности и конденсатор обмениваются энергией, и вся потребляемая от источника мощность выделяется на активном сопротивлении в виде джоулева тепла. Напряжения на индуктивности и емкости равны друг другу и изменяются в противофазе (см. векторную диаграмму на рис. 15.1), поэтому этот режим работы называется резонансом напряжений. Амплитуда силы тока . При резонансе напряжений напряжение на активном сопротивлении равно ЭДС источника, однако напряжения на индуктивности и емкости могут значительно превышать ЭДС.

При параллельном включении конденсатора, катушки индуктивности и внешней ЭДС, как показано на рисунке 15.2, возникает резонанс токов. В этом случае напряжения на катушке и конденсаторе все время одинаковы и равны внешней ЭДС. Однако сила тока, протекающего через катушку и конденсатор, зависит от частоты и на определенной частоте принимает максимальное значение. При параллельном включении импеданс цепи будет определяться выражением

, (15.6)

где 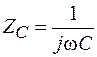– реактивное сопротивление конденсатора; 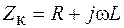– сопротивление катушки; – мнимая единица. Подставляя эти выражения в (15.6), получим

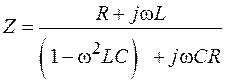. (15.7)

Резонанс токов возникает, когда импеданс цепи становится чисто активным, а индуктивное и емкостное сопротивления равны друг другу. Приравнивая нулю мнимую часть выражения (15.7), легко получить, что резонансная частота

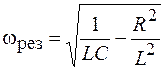. (15.8)

При малых потерях можно считать, что 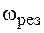совпадает с частотой собственных колебаний 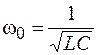. Из (15.7) следует, что импеданс цепи при этих условиях принимает максимальное значение 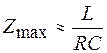и неограниченно возрастает при уменьшении активного сопротивления.

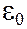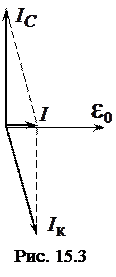Вынужденные колебания при параллельном включении контура изображают с помощью векторной диаграммы токов (рис. 15.3). Отложим в горизонтальном направлении вектор . Ток через конденсатор опережает напряжение на нем на и изобразится вектором 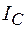. Если бы активное сопротивление катушки было равно нулю, то сила тока в катушке отставала бы от напряжения по фазе на . Вследствие наличия активного сопротивления отставание будет отличаться от , но при малом 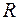это отличие будет незначительным, и ток в катушке изобразится вектором 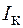, почти противоположным по направлению вектору 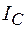. Полный ток 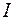равен сумме токов 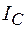и . При резонансе токов сила тока, протекающего через конденсатор и катушку индуктивности, имеет максимальное значение, значительно превышающее силу тока, протекающего через источник.

Вынужденные колебания и явление резонанса широко используются в радиотехнике. Принимаемые антенной радиостанции электромагнитные волны возбуждают во входном LC -контуре вынужденные колебания, которые затем усиливаются и после электронной обработки преобразуются в передаваемое сообщение. LC -контур имеет конденсатор переменной емкости (либо катушку переменной индуктивности), с помощью которого можно изменять резонансную частоту. За счет этого радиостанция настраивается на заданную частоту и осуществляет прием сигналов от конкретного передатчика. В результате резонанса амплитуда полезного сигнала принимает максимальное значение и одновременно происходит подавление помех, частота которых отлична от резонансной.

Дата добавления: 2014-01-05