Ротор вектора. Теорема Стокса

Пусть задано поле вектора . Выберем в пространстве произвольную точку 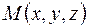и контур L (рис. 34.1). Возьмем некоторую поверхность S, ограниченную контуром L и проходящую через точку M. Обозначим площадь этой поверхности 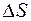. Зададимся произвольно направлением обхода контура и найдем циркуляцию 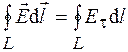вектора по контуру L. Эта циркуляция будет зависеть от характеристик поля, размеров, формы и ориентации в пространстве контура L. Составим отношение циркуляции вектора по контуру L к площади поверхности, ограниченной этим контуром:

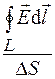. (34.1)

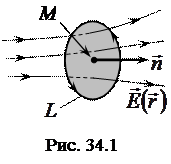Будем стягивать контур L в точку M таким образом, чтобы площадь поверхности 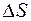стремилась к нулю, но при этом точка M оставалась на поверхности S. Можно ожидать, что отношение (34.1) будет стремиться к некоторому пределу, который не будет зависеть от размеров и формы контура L и поверхности S, а будет определяться только характеристиками поля в точке M и ориентацией контура в пространстве. Пусть 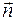– единичный вектор правой нормали к поверхности S. Если предел отношения (34.1) при указанных условиях существует, то он равен проекции некоторого вектора на направление правой нормали к контуру L, т. е.

.

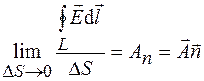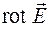Определенный таким образом вектор называется ротором вектора и обозначается , т. е. проекция ротора вектора на направление правой нормали к контуру L определяется соотношением

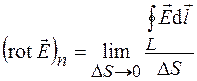. (34.2)

Из (34.2) следует, что ротор вектора будет отличен от нуля, если циркуляция вектора не равна нулю, т. е. поле вектора является вихревым. Символ "rot" происходит от сокращенного латинского слова rotatio – вращение. Если вектор задан своими проекциями в декартовой системе координат 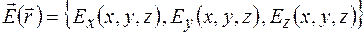, то проекции 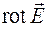на координатные оси определяются выражениями

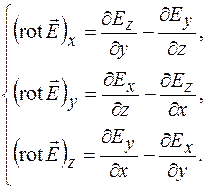(34.3)

В математике доказывается теорема Стокса, в соответствии с которой циркуляция вектора по контуру L равна потоку ротора вектора через поверхность S, ограниченную контуром L, при условии, что направление обхода контура и нормаль к поверхности связаны правилом правого винта:

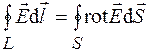. (34.4)

Дата добавления: 2014-01-05