КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула трапеції
|
|
|
|
Розіб'ємо інтервал інтегрування на n рівних частин, кожна довжиною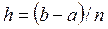 
. Площа однієї частини є визначений інтеграл від хі до хі+1:
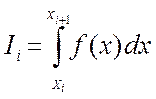(1.9)
Але якщо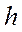 
досить мала, то площу ділянки можна визначити як площу трапеції АВС (рис. 1.9) так що
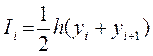(1.10)
Значення інтеграла одержуємо як суму площ: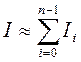 
або зважаючи, що внутрішні ординати в сумі площ повторюються двічі, запишемо:
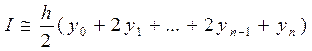(1.11)
Ця формула в компактній формі записується так:
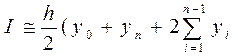(1.13)
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 317; Нарушение авторских прав?; Мы поможем в написании вашей работы!