
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение линейной модели парной регрессии
Пример
По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Х, млн. руб.).
| Y | |||||||
| X |
Требуется:
1.Для характеристики Y от Х построить следующие модели:
· линейную (для сравнения с нелинейными),
· степенную,
· показательную,
· гиперболическую.
2.Оценить каждую модель, определив:
· индекс корреляции,
· среднюю относительную ошибку,
· коэффициент детерминации,
· F-критерий Фишера.
3.Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.
4.Рассчитать прогнозные значения результативного признака по лучшей модели, если объем капиталовложений составит 89,573 млн. руб.
5.Результаты расчетов отобразить на графике.
Решение:
Определим линейный коэффициент парной корреляции по следующей формуле:
 ;
;
Можно сказать, что связь между объемом капиталовложений Х и объемом выпуска продукции Y обратная, достаточно сильная.
Уравнение линейной регрессии имеет вид: ŷ = a + b ´ x
Таблица 3.5
| t | y | x | y´x | x´x | 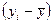
| 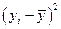
| 
|  2 2
| 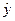
| 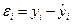
| 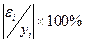
|
| 13.43 | 180.36 | -17.4 | 303.8 | 60.2 | 3.84 | 6.000 | |||||
| 5.43 | 29.485 | -13.4 | 180.36 | -1.96 | -3.500 | ||||||
| 1.43 | 2.0449 | 0.57 | 0.3249 | 50.3 | 1.74 | 3.346 | |||||
| -2.57 | 6.6049 | -5.43 | 29.485 | 53.6 | -5.56 | -11.583 | |||||
| -0.57 | 0.3249 | 2.57 | 6.6049 | 49.2 | 0.84 | 1.680 | |||||
| -4.57 | 20.885 | 14.57 | 212.28 | 42.6 | 3.44 | 7.478 | |||||
| -12.6 | 18.57 | 344.84 | 40.4 | -2.36 | -6.211 | ||||||
| итого | 0.01 | 397.71 | 1077.7 | -0.02 | 39.798 | ||||||
| ср.знач | 50.57 | 81.43 | 4033.14 | 6784.57 | 5.685 | ||||||
| диспер | 56.8 |
Значения параметров a и b линейной модели определим, используя данные таблицы 3.5
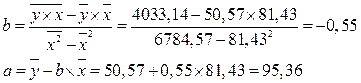
Уравнение линейной регрессии имеет вид:
ŷ = 95,36 - 0,55 ´ х
С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции уменьшится в среднем на 550 тыс. руб.
Это свидетельствует о неэффективности работы предприятий, и необходимо принять меры для выяснения причин и устранения этого недостатка.
Рассчитаем коэффициент детерминации:
R2 = r2yx = 0,822
Вариация результата Y (объема выпуска продукции) на 82,2 % объясняется вариацией фактора Х (объемом капиталовложений).
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:
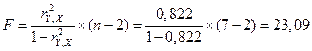
F>FТАБЛ = 6,61 для a = 0,05; к1=m=1, k2=n-m-1=5.
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F>FТАБЛ .
Определим среднюю относительную ошибку:
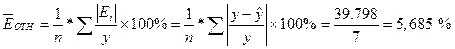
В среднем расчетные значения ŷ для линейной модели отличаются от фактических значений на 5,685 %.
|
Дата добавления: 2014-01-05; Просмотров: 2131; Нарушение авторских прав?; Мы поможем в написании вашей работы!