Доверительная вероятность и доверительный интервал

Все рассмотренные выше оценки неизвестного параметра 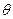, найденные по выборке объёма « n» из генеральной совокупности не позволяют ответить на вопрос, какую ошибку мы совершаем, принимая вместо точного значения неизвестного параметра 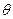некоторое его приближённое значение (оценку) .

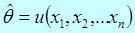Поэтому,при выборке малого объематочечная оценка может значительно отличаться от оцениваемого параметра,т. е. приводить к грубым ошибкам. По этой причинепри небольшом объеме выборкиследует пользоватьсяинтер­вальными оценками.

Интервальной оценкой неизвестного параметра 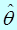называют статистическую оценку, определяемую двумя числам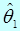и и 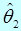- концами интервала, накрывающего оцениваемый параметр.

Иногда пользуются более кратким определением интервальной оценки.

Интервальной называютоценку, которая определяется двумя числами—концами интервала.

Интервальные оценки позволяют установить точность и надежность оценок.

Рассмотрим смысл этих понятий для статистических оценок.

Пустьнайденная по данным выборкистатистическая характеристика (оценка) 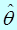служит оценкой неизвестного параметра 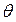. Будем считать 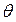постоянным числом (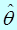может быть и случайной величиной).Очевидно, чточем точнее 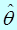определяет параметр 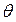,тем лучше качество оценки, тем меньше абсолютная величина их разности .

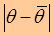Таким образом, качество статистической оценки по такому показателю качества, как точность, определяется неравенством вида:

(4.1)

где - положительное число.

Другими словам и – чем меньше , тем точнее статистическая оценка неизвестного параметра. Отсюда следует, что положительное число δ характеризует точность оценки.

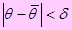Однако, статистические методы не позволяют категорически утверждать, что оценка 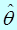удовлетворяет неравенству

Поэтому, можно лишь говоритьо вероятности 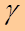, с которой это неравенство выполняется. Эту вероятность называют доверительной вероятностью.

Доверительной вероятностью (надёжностью оценки) называют вероятность 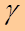, с которой выполняется неравенство .

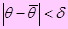Обычнодоверительная вероятность (надёжность)задаётся заранее, причём численное значение этой вероятности 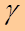берут число близкое к единице.Наиболее часто задают доверительную вероятность, равной: 0,95; 0,99, 0,9973, 0,999.

Запишем выражение, определяющее доверительную вероятность, согласно её определения, а именно:

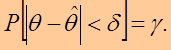(4.2)

Заменив в выражении (4.2) неравенство 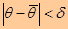равносильнымемудвойным неравенством или 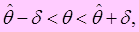получим:

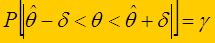(4.3)

Полученное выражениедоверительной вероятности (4.3)говорит о том, что,с вероятностью 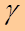неизвестное значение параметра 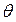попадёт в интервал:

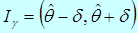(4.4)

Интервал, описываемый выражением (4.4), называют доверительным интервалом. Поэтому можно дать следующее определение:

Доверительным интервалом называется интервал 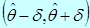, накрывающий неизвестный параметр 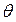с заданной доверительной вероятностью.

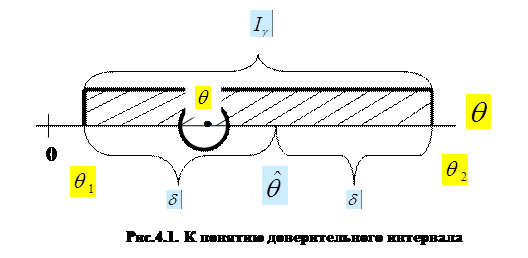
Для пояснения понятия доверительного интервала следует отметить следующее важное обстоятельство.

Ранее неоднократно рассматривалась вероятность попадания случайной величины в заданный неслучайный интервал. В данном случае дело обстоит иначе: величина 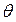неслучайна, зато случаен интервал 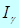. Случайность этого интервала объясняется следующим: 1) случайно его положение, определяемое его центром 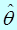; 2) случайна длина интервала , так как величина вычисляется, как правило, по опытным данным (определяется объёмом выборки n ).

Поэтому в данном случаелучше будет толковатьвеличину 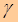не как вероятность «попадания» точки 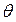в интервал 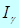, а как вероятность того, что случайный интервал 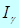накроет точку 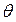.Геометрическое толкование данного обстоятельства представлено на Рис.4.1.

Дата добавления: 2014-01-05