
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системи числення з ірраціональними основами
|
|
|
|
У спеціалізованих обчислювальних засобах знаходять застосування двійково-кодовані системи числення з ірраціональними основами, до яких відносять так звані р- коди Фібоначчі і коди “золотої” р -пропорції. При цьому р -кодом Фібоначчі називають представлення числа у вигляді
 ,
,
де 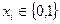 – двійкова цифра в і -му розряді,
– двійкова цифра в і -му розряді, 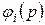 - вага
- вага  -го розряду, визначена як
-го розряду, визначена як
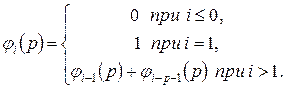
Таким чином, вага 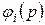 залежить як від його позиції
залежить як від його позиції  в записі числа, так і від параметра р.
в записі числа, так і від параметра р.
Якщо р=0, то р- код Фібоначчі збігається з представленням числа в двійковій канонічній системі числення
У випадку р=1 код Фібоначчі відповідає системі числення зі штучним порядком ваг, а саме: 1,1,2,3,5,8,13, 21,34,... У цій послідовності будь-яка вага дорівнює сумі двох попередніх ваг.
Якщо р=2, то послідовність ваг р- коду Фібоначчі має вигляд 1,1,1,2,3,4,6, 9,13,19,28,....
При 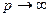 подібна послідовність складається з р одиниць, після яких слідує натуральний ряд чисел. Як і в інших системах зі штучним порядком ваг, представлення чисел р -кодами Фібоначчі не є однозначним. До числа основних достоїнств кодів Фібоначчі слід віднести і підвищення швидкодії при виконанні деяких типів операцій і зручність організації контролю правильності їхнього виконання.
подібна послідовність складається з р одиниць, після яких слідує натуральний ряд чисел. Як і в інших системах зі штучним порядком ваг, представлення чисел р -кодами Фібоначчі не є однозначним. До числа основних достоїнств кодів Фібоначчі слід віднести і підвищення швидкодії при виконанні деяких типів операцій і зручність організації контролю правильності їхнього виконання.
Кодом “золотої” р -пропорції називають представлення числа у вигляді

де 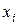 – двійкова цифра в
– двійкова цифра в  -му розряді,
-му розряді, 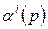 - вага
- вага  -го розряду, причому
-го розряду, причому
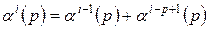 .
.
Наведене представлення задає нескінченне число способів нумерації дійсних чисел, тому що кожному 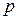 тут відповідає свій спосіб нумерації. Ваги розрядів у такому представленні зв'язані з вагами розрядів у
тут відповідає свій спосіб нумерації. Ваги розрядів у такому представленні зв'язані з вагами розрядів у 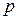 -кодах Фібоначчі наступним співвідношенням
-кодах Фібоначчі наступним співвідношенням
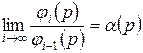 .
.
Звідси при р=0 випливає 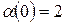 , тобто, код “золотий’
, тобто, код “золотий’ 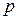 -пропорції відповідає в цьому випадку двійковій позиційній однорідній системі числення. При р>0 значення
-пропорції відповідає в цьому випадку двійковій позиційній однорідній системі числення. При р>0 значення 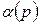 є ірраціональним числом. Зокрема для р= 1
є ірраціональним числом. Зокрема для р= 1

Це число було відоме ще древнім грекам з розв’язання задачі про поділ відрізка в середнім і крайнім відношеннях. У середні віки таке пропорційне відношення було названо “золотим”. Цим і пояснюється походження назви кодів. Подібно 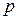 -кодам Фібоначчі особливістю кодів “золотий”
-кодам Фібоначчі особливістю кодів “золотий” 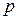 -пропорції є неоднозначність представлення дійсних чисел, за винятком нуля. Крім того, при р>0 поняття цілого і дробового числа в таких кодах не збігаються з загальноприйнятими. Наприклад, ціле число 3 у коді “золотої” 1-пропорції зображується як 100,01, а ірраціональне число
-пропорції є неоднозначність представлення дійсних чисел, за винятком нуля. Крім того, при р>0 поняття цілого і дробового числа в таких кодах не збігаються з загальноприйнятими. Наприклад, ціле число 3 у коді “золотої” 1-пропорції зображується як 100,01, а ірраціональне число 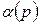 при будь-якому р>0 зображується так само, як і основа числення в канонічній двійковій системі, тобто, як 10.
при будь-якому р>0 зображується так само, як і основа числення в канонічній двійковій системі, тобто, як 10.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 364; Нарушение авторских прав?; Мы поможем в написании вашей работы!