Шифры простой перестановки

Блочные шифры

В связи с тем, что открытый текст сообщения обычно имеет произвольную длину, иногда достаточно большую, то он разбивается на более мелкие блоки фиксированной длины. Тексты этих блоков шифруются отдельно и независи­мо друг от друга.

Одноключевые блочные шифры подразделяются на 3 группы:

• Шифры перестановки

• Шифры замены (подстановки)

• Составные шифры.

При использовании шифров перестановки, которые предназначены для ус­транения смысла сообщения путем изменения порядка чередования его сим­волов, знаки открытого текста переставляются по некоторому правилу (клю­чу) в пределах заданного блока. В результате этого нарушается нормальный порядок их следования и сам смысл информационного сообщения. При этом различают шифры простой и сложной перестановки.

Шифр простой перестановки переупорядочивает группу букв текста регу­лярным образом в соответствии с выбранным ключом (правилом) переста­новки. Из истории известно множество примеров использования таких шиф­ров для ручного шифрования. При этом часто использовались специальные таблицы, которые давали простые шифрующие процедуры (ключи), согласно которым производились перестановки букв в сообщении. Ключом у таких таб­лиц служили размеры таблицы, фраза, задающая перестановку или другие специальные особенности таблицы.

Пример простейшего шифра перестановки представлен на рис. 5.5.

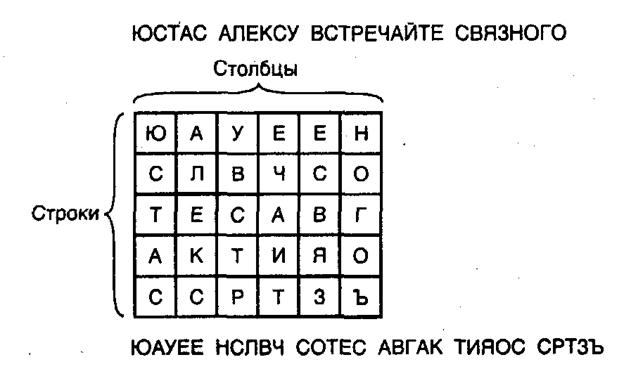
Рис. 5.5. Простейший шифр перестановки.

Как видно из рис. 5.5, для того чтобы зашифровать сообщение «ЮСТАС АЛЕКСУ ВСТРЕЧАЙТЕ СВЯЗНОГО», последнее необходимо записать в виде таблицы, состоящей, например, их 5 строк и 6 столбцов. Текст сообщения записы­вается по столбцам, исключая пробелы. Если последний стол­бец оказывается неполным, он заполняется произвольно лю­быми буквами. Для получения зашифрованного сообщения ис­ходный текст считывается по­строчно (слева направо) и за­писывается группами, напри­мер, по 5 цифр. Последняя

процедура не относится к процессу шифрования и делается только для того, чтобы было удобнее записывать текст, лишенный всякого смысла. Для рас­шифрования такого текста необходимо знать ключ, а именно количество строк и столбцов в таблице или иными словами, ее размер.

Более практический метод шифрования, очень похожий на предыдущий, опи­сывается ниже. Он отличается лишь тем, что колонки таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.

При шифровании простой перестановкой шифруемый текст последова­тельными строками записывается под символами ключевого слова, кото­рые не должны повторяться Для упрощения запоминания ключа использу­ют ключевое слово, буквы которого, пронумерованные в порядке их рас­положения в алфавите, задают правило перестановки. Зашифрованный текст выписывается колонками в той последовательности, в которой располага­ются в алфавите буквы ключа или в порядке следования цифр в натураль­ном ряду, если ключ цифровой. Наглядно процесс шифрования с использо­ванием шифра простой перестановки представлен на рис. 5.6. Предполо­жим, что необходимо зашифровать информационное сообщение

«ЗАСЕДАНИЕ СОСТОИТСЯ ЗАВТРА ЮСТАС».

Для шифрования этого открытого текста запишем его без пробелов (уча­стие последних в процедуре шифрования, из-за их высокой частоты повто­рения, значительно ослабляет криптостойкость шифра) и выберем ключ шифрования, например, 245 136. Согласно этому ключу, состоящему из 6 цифр, поделим все информационное сообщение на блоки, каждый из кото­рых будет содержать по 6 букв текста. После деления на блоки у нас полу­чилось 4 блока, содержащих по 6 букв в каждом, и 1 блок — по 5 букв. В таких случаях последняя группа букв исходного сообщения произвольно дополняется различными символами до получения полного блока. В на­шем случае не достает только одной буквы, поэтому выбираем любую букву, например Ъ, и добавляем ее в конце пятого блока.

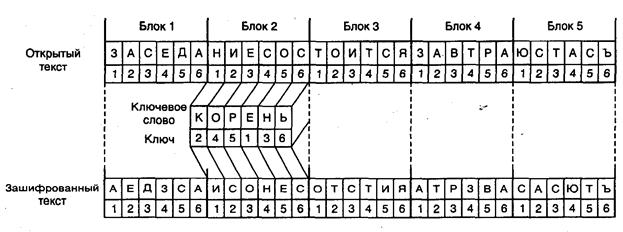
Рис. 5.6. Шифр простой перестановки

Далее, используя ключ 245 136, производится перестановка букв исходно­го открытого текста. Например, первая цифра ключа — 2, указывает на то, что в новом блоке первой буквой зашифрованного текста будет вторая буква бло­ка открытого текста, вторая цифра ключа — 4, показывает, что вторая буква шифротекста — это четвертая буква в блоке открытого текста и т. д.

В конечном итоге, после проведения перестановок во всех блоках, по­лучаем зашифрованный текст. Прочитав его, мы видим, что он полностью лишен какого-либо смыслового содержания.

Для упрощения запоминания ключа обычно используется ключевое слово. В данном случае — это слово «КОРЕНЬ». В нем цифре 1 ключа соответ­ствует буква Е, так как она первой из всех букв этого слова встречается в нашем алфавите, цифре 2 — буква К (по той же причине) и т. д.

То же сообщение можно зашифровать с использованием таблицы, состоя­щей, например, из 5 строк и 6 столбцов (по длине ключевого слова). Исход­ный текст записывается по столбцам и образует таблицу (рис. 5.7). Ключевое слово задает правило перестановки столбцов. Если в ключевом слове встре­чаются одинаковые буквы, то они нумеруются по порядку слева направо. По­лученный второй шифротекст, как это видно из рис. 5.7, совершенно не похож на первый.

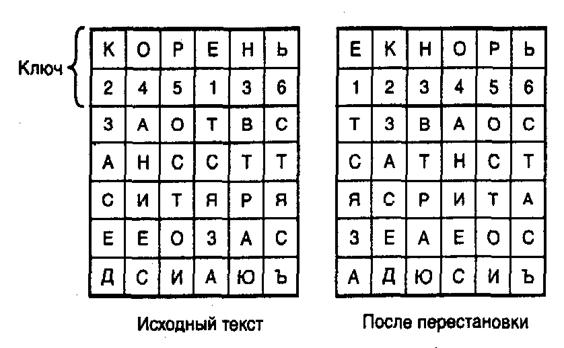
Рис. 5.7. Шифрование с помощью таблицы

Основным недостатком данного шифра является его невысокая криптостойкость. Разложив зашифрованный текст на множители (не так уж мно­го получается вариантов), можно легко определить вероятную длину кодо­вого слова, которое использовалось при шифровании.

Для повышения криптостойкости полученного выше шифрованного тек­ста можно попробовать зашифровать его еще раз. Этот способ шифрования известен под названием двойная перестановка. Суть этого способа заключа­ется в следующем. Полученный после первого шифрования текст шифрует­ся вторично с использованием таблицы с другой размерностью (длины строк и столбцов подбираются другими). Кроме того, в одной таблице можно пе­реставлять строки, а в другой столбцы. Заполнять таблицу исходным тек­стом можно разными способами: зигзагом, змейкой, по спирали и т. п.

Шифр простой перестановки с использованием свойств таблиц, назы­ваемых магическими квадратами (рис. 5.8), использовался еще в средние века. Магическими квадратами называются равносторонние таблицы, все клетки которых заполнены натуральными числами, начиная от 1. При­чем эти числа в сумме дают по каждому столбцу, по каждой строке и по диагоналям магического квадрата одно и тоже число (в нашем случае — это число 34). Исходный текст — ЖДУ ВСТРЕЧИ ЮСТАС, при заполне­нии магического квадрата, вписывается по порядку следования натураль­ных чисел, например, число 1 заменялось 1 буквой исходного текста (Ж), число 12 — 12 буквой сообщения (С) и т.п. После записи открытого тек­ста содержимое таблицы считывается по строкам в результате чего и получался шифротскст с перестановкой букв.

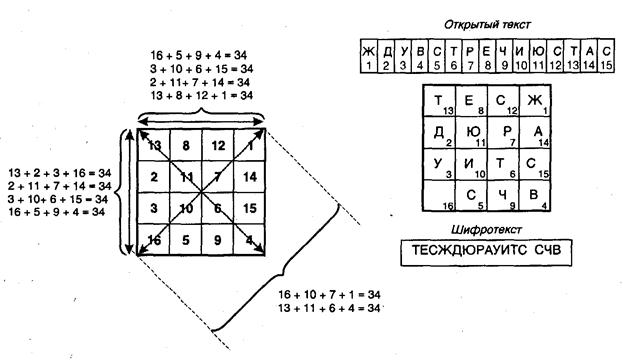
Рис. 5.8. Магический квадрат

Дата добавления: 2014-01-05