Синхронные поточные шифры

В синхронных поточных шифрах ключевая последовательность или, как ее еще называют, гамма, формируется независимо от последователь­ности символов открытого текста и каждый символ этого текста шифру­ется независимо от других символов, а ключом Z является начальная ус­тановка генератора ПСП. Процесс шифрования и расшифрования при этом описывается выражениями:

Y_i = X_i Е F_i (Z) — шифрование;

X_i = Y_i Е F_i (Z) — расшифрование,

где Y_i, X_i — двоичные символы зашифрованного и открытого текста, F_i (Z) — i-й символ ПСП, вырабатываемый генератором с функцией об­ратной связи F и начальным состоянием Z; Е – оператор объединения символов зашифрованного и открытого текста.

Синхронные поточные шифры можно классифицировать по способам построения ПСП, по соотношению размеров открытого текста и периода ключевой ПСП, по способам технической реализации (рис. 5.19).

По способам построения ПСП для синхронного шифрования различают:

• Метод комбинирования ПСП

• Метод функциональных отображений.

Суть первого метода заключается в построении комбинированных схем, представляющих собой совокупность регистров сдвига с линейными обрат­ными связями. Примерами таких схем являются схема Джеффра (рис. 5.20 а) и схема Брюс (рис. 5.20 б).

Отличие этих двух схем состоит в использовании для формирования ПСП различных логических устройств. Так, в схеме Джеффа применяется операция логического умножения и сложения по модулю 2. Схема Брюс использует пороговое устройство, работающее по правилу: на выходе 1, если порог превышен, иначе — 0.

Более сложным является метод функциональных отображений, суть ко­торого заключается в следующем. Пусть дано некоторое векторное про­странство GF(2^m) с числом координат m в каждом векторе, причем каждая координата вектора принадлежит множеству скалярных величин GF(2)={0,l}. Очевидно, что общее число векторов, принадлежащих про­странству GF(2^m), равно 2^т. Пусть задано некоторое функциональное ото­бражение f, которое каждому вектору из векторного пространства GF(2^m) ставит в соответствие вектор из пространства GF(2^k). При этом обязатель­ным является выполнение условия k<=m. Далее пусть задано некоторое функциональное отображение g, которое каждому вектору из GF(2^k) ста-

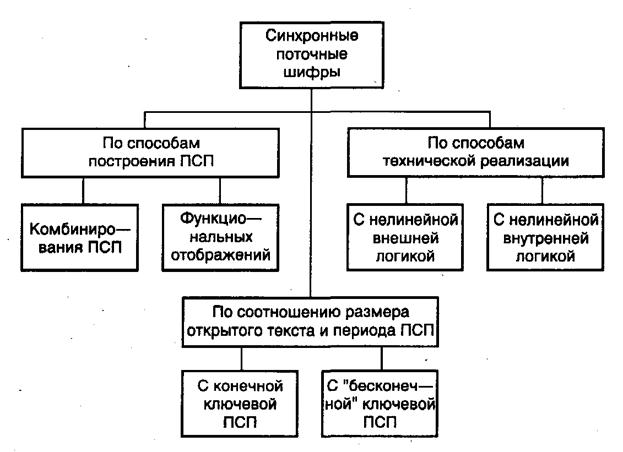
Рис. 5.19. Классификация синхронных поточных шифров

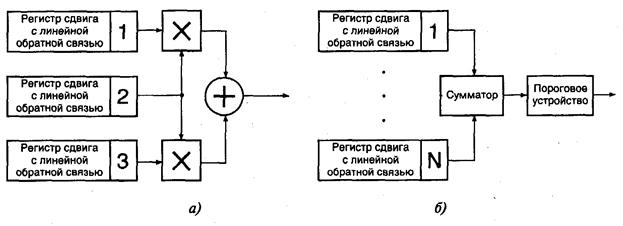
Рис. 5.20. Схема Джеффа (а) и схема Брюс (б)

вит в соответствие скаляр из множества GF(2). В этом случае получим ПСП с использованием вышеприведенных функциональных отображений. Например, ПСП, полученная по схеме, изображенной на рис. 5.21 (m = 4, k = 2), построена по методу двухступенчатых отображений.

Метод ступенчатого отображения GF(2^m) — GF(2^k) — GF(2) впервые был использован при построении последовательностей Гордона-Милса-Велга. Для порождения векторного пространства GF(2^m) использовались регистры сдвига с линейными обратными связями длины m с обратной свя­зью.

Следует заметить, что на практике имеет место различное число функцио­нальных отображений. С возрастанием используемых ступеней уровень криптостойкости шифрования повышается.

По отношению размера открытого текста и периода ключевой ПСП разли­чают схемы:

• С «бесконечной» ключевой ПСП (период ПСП больше размера открытого текста)

• С конечной ключевой ПСП или с режимом «бегущего кода» (пе­риод ПСП равен размеру открытого текста).

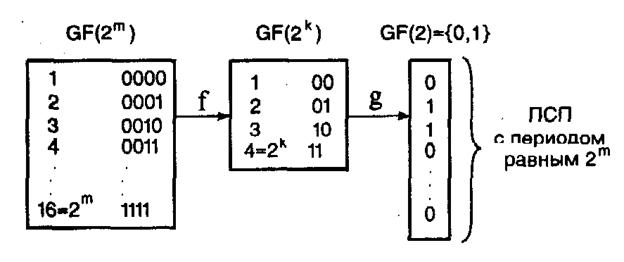
Рис. 5.21. Принцип формирования ПСП по методу двухступенчатых отображений

Рис. 5.22. Схема с нелинейной внешней (а) и внутренней (6) логикой

Схемы с «бесконечной» ключевой ПСП обладают более высокой криптостойкостью относительно вскрытия их структуры при известном откры­том тексте. Однако при вскрытии структуры ПСП по частично известному тексту схема «бегущий код» не позволяет вскрывать весь текст, а только его небольшую часть, поэтому, например, разработчики спутниковой системы «На-встар» в качестве криптостойкой ПСП Р-кода использовали сегменты дли­тельностью 7 суток, выделенные случайным образом из нелинейной ПСП с периодом 267 суток.

По способам технической реализации синхронных поточных шифров можно выделить схемы, представленные на рис. 5.22:

• с нелинейной внешней логикой

• с нелинейной внутренней логикой.

При использовании нелинейной внешней логики основу генератора ПСП составляет регистр сдвига с линейными обратными связями, который по­рождает все ненулевые элементы векторного пространства GF(2ⁿ).

В схеме с нелинейной внутренней логикой генератор ПСП представля­ет собой регистр с нелинейными обратными связями. Такой генератор вы­рабатывает последовательности де Брейна с периодом 2 ⁿ. Такие последо­вательности обладают одними из самых высоких показателей криптостойкости из всех классов ПСП, так как каждая серия из n-символов встречается на периоде ПСП только один раз.

Дата добавления: 2014-01-05