Линейный криптоанализ

Метод линейного криптоанализа впервые был применен для атаки блочного шифра FEAL [376] и затем DES [377]. Данный метод использует линейные приближения. Это озна­чает, что, если выполнить операцию XOR над некоторыми битами открытого текста, затем над некоторыми битами шифротекста, а затем выполнить XOR результатов предыдущего суммирования, можно получить бит, который равен сумме некоторых бит ключа. Это назы­вается линейным приближением, которое может быть верным с некоторой вероятностью р. Если р ¹ 0,5, то этот факт можно использовать для раскрытия бит ключа.

Рассмотрим данный метод подробнее. Пусть в общем виде линейное выражение задается уравнением:

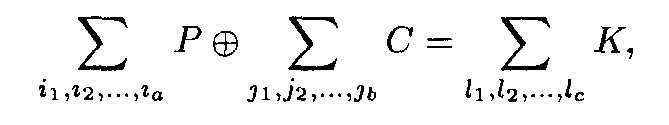
(3..1)

где i ₁, i ₂,…, i _a, j ₁, j ₂,…, j _b, и l _1, l _2,…, l _c, позиции некоторых бит открытого текста Р, шиф­ротекста С и ключа К. (Напомним, что суммирования в (3.1) выполняется по модулю 2) Для случайно выбранного открытого текста Р и соответствующего шифротекста с уравне­ние (3.1) выполняется с вероятностью р ¹ 1/2. Величина |р-1/2| определяет эффективность уравнения (31).

Таким образом, при заданном эффективном линейном выражении можно определить один бит ключа К, воспользовавшись следующим алгоритмом максимума правдоподобия:

Алгоритм 1.

Шаг 1. Пусть T задает число открытых текстов, таких, что левая часть уравнения (3.1) равна нулю.

Шаг 2. Тогда, если T > N /2 (N — общее число открытых текстов),

угадываем

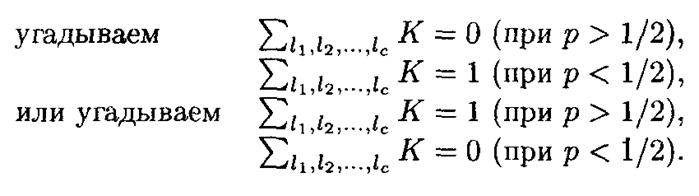
Вероятность успеха увеличивается с ростом N или |р — 1/2|.

Рассмотрим криптоалгоритм DES с n -циклами криптографического преобразования. С учетом 48-битного ключа К _n и F -функции линейное выражение принимает следующий вид:

(3.2)

где через С^R обозначена правая половина блока шифротекста.

Оценивая эффективность уравнения (3.2) при подстановке различных кандидатов, можи восстановить К_n и 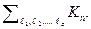Для этого следует воспользоваться следующим алгоритмом максимального правдоподобия:

Алгоритм 2.

Шаг 1. Пусть Т задает число открытых текстов, таких, что левая часть уравнения (3.2 равна нулю для каждого кандидата К_n ^{( i )} (i = 1,2,...).

Шаг 2. Обозначим через Т _mах и Т _min максимальное и минимальное значения среди T_i.

Тогда

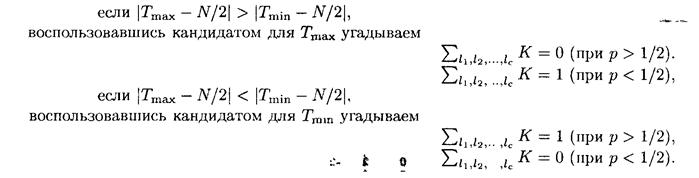
Рассмотрим линейные приближения для S -блоков. Задача заключается в исследовании вероятности того, что некоторый бит на входе S -блока равняется некоторому биту на выхо­де. Однако в более общем случае полезно рассмотреть зависимости сумм бит на некоторых входных и выходных позициях.

Для заданного S -блока S_a (a = 1,2,..., 8) и чисел 1£ a £63и1£ b £15 определим NSa (a, b) - число выходных значений для 64 возможных значений на входе S_а, таких, что результат логической операции «И» суммы по модулю 2 некоторых бит значения на входе S_а и числа a равен результату логической операции «И» суммы по модулю 2 некоторых бит значения на выходе S_а и числа b. Данное условие можно записать в виде:

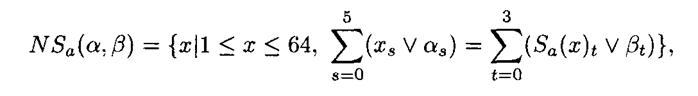
(3.3)

где S_a (x) _t — t-й бит выходного значения S_a при заданном на входе значении х.

Если NSa (a, b) не равно 32, можно сделать вывод о корреляционной зависимости вход­ных и выходных бит S_a. Например, уравнение 3.4 показывает, что четвертый бит входных значений S₅ равен сумме всех бит выходных значений с вероятностью 12/64 = 0,19:

NS₅ (16, 15)=12. (3.4)

Следующее уравнение выполняется с вероятностью 0,19 для случайно выбранного X и зафиксированного К (с учетом перестановки в Е - и Р -блоках):

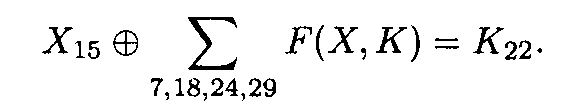(3.5)

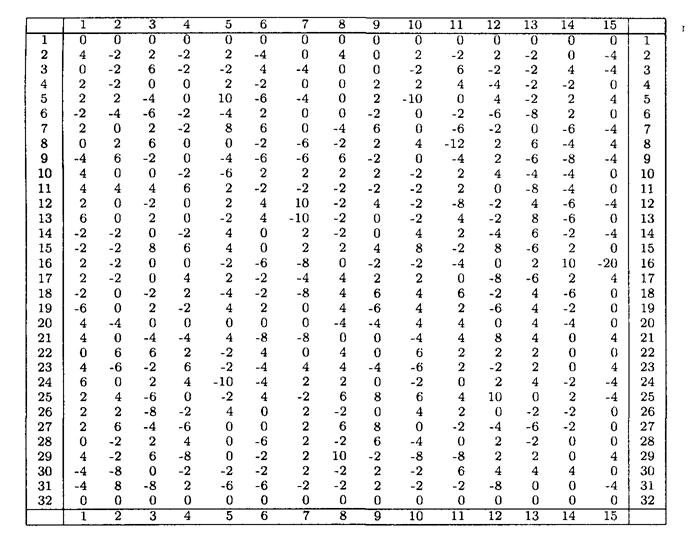
В усеченной табл. 3.19 представлены значения NS₅ (a, b) - 32 для всевозможных значе­ний a (номер строки) и b (номер столбца). Исследование полной таблицы показывает, что уравнение (3.4) является наилучшим линейным приближением во всех S -блоках (то есть величина | NS₅ (a, b)| принимает максимальное значение). Следовательно, уравнение (3.4) является наилучшим линейным приближением для F -функции.

Из определения S -блоков вытекает, что

(1) NSa (a, b) четно;

(2) если a = 1,32 или 33, то NSa (a, b) = 32 для всех Sa и Sa.

Рассмотрим криптоалгоритм DES с тремя циклами преобразования. Следующее уравне­ние выполняется для первого цикла с вероятностью 12/64:

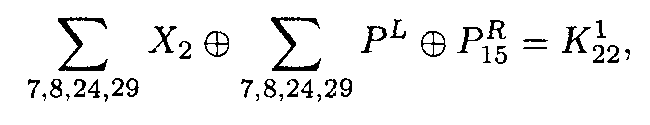(3.6)

где через P^R и P^L обозначены правая и левая половины открытого текста. Аналогичное уравнение выполняется для последнего третьего цикла преобразования:

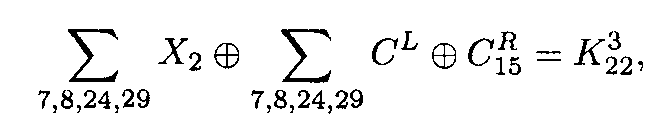(3.7)

где через C^R и C^L обозначены правая и левая половины шифротекста.

Таблица 3.19 - Криптоанализ DES: усеченная таблица значений NS₅ (a, b) - 32

Таким образом, линейное приближение для третьего цикла выглядит следующим образом:

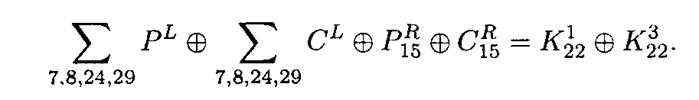(3.8)

Для случайно выбранного открытого текста Р и соответствующего шифротекста С урав­нение (3.8) выполняется с вероятностью (12/64)² + (1 - 12/64)² = 0,70. Поскольку уравне­ние (3.5) является наилучшим линейным приближением F -фун-кции, уравнение (3.8) явля­ется наилучшим приближением для DES с тремя циклами. Теперь, воспользовавшись Алго­ритмом 1, можно решить уравнение (3.8) для того, чтобы получить значение К¹₂₂ ÅК³₂₂

Описанный метод можно обобщить на полный DES с шестнадцатью циклами криптогра­фического преобразования.

Дата добавления: 2014-01-05