С распределенным лагом. Метод Алмон

ОЦЕНИВАНИЕ ПАРАМЕТРОВ МОДЕЛЕЙ

Ниже мы опишем суть метода Алмон.

1. Формализуют зависимость коэффициентов b_j от величины лага j. Модель зависимости представляет собой полином:

• либо 1-й степени: ;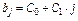

• либо 2-й степени: ;

• либо 3-й степени: ;

• • либо K -й степени (общий случай):
.

2. Тогда каждый коэффициент модели (11) – b_j
(j = 0; L) можно выразить следующим образом:

;

;

;

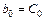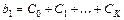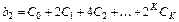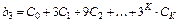и т.д.

.

Подставим найденные соотношения для b_j в модель (11) и получим:

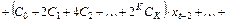
3. Перегруппируем слагаемые:

.

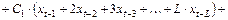
Обозначим слагаемые в скобках при коэффициентах C_i (i=0; K) как новые переменные:

;

;

;

…

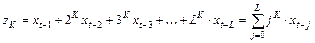
Тогда модель примет вид:

. (12)

4. Определим параметры новой модели (12) с помощью обычного МНК. Затем от параметров
С_i (i = 0; К) перейдем к параметрам b_j (j = 0; L), используя соотношения, полученные на 1-м шаге.

Лекция №39

ОЦЕНИВАНИЕ ПАРАМЕТРОВ МОДЕЛЕЙ С ГЕОМЕТРИЧЕСКОЙ СТРУКТУРОЙ ЛАГА.

МЕТОД КОЙКА

Лекция №40

ОЦЕНИВАНИЕ ПАРАМЕТРОВ МОДЕЛЕЙ

АВТОРЕГРЕССИИ.

МЕТОД ИНСТРУМЕНТАЛЬНЫХ ПЕРЕМЕННЫХ

При построении моделей авторегрессии:

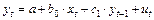(15)

Лекция №41

МОДЕЛЬ АДАПТИВНЫХ ОЖИДАНИЙ

В общем виде модель адаптивных ожиданий можно за писать так:

. (17)

адаптивных ожиданий следующий:

или . (18)

Подставим в модель (17) вместо соотношение (18):

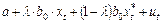. (19)

Если модель (17) имеет место для периода t, то она будет иметь место и для периода (t – 1). Таким образом, в период (t–- 1) получим:

.

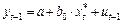Умножим это выражение на (1 – l) и получим:

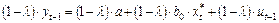
Вычтем почленно полученное выражение из (19):

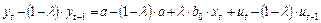или ,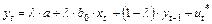

где .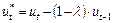

Лекция №42

МОДЕЛЬ ЧАСТИЧНОЙ (НЕПОЛНОЙ) КОРРЕКТИРОВКИ

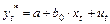. (20)

или (21)

Дата добавления: 2014-01-05