Равномерное распределение U(a,b)

Законы распределения и числовые характеристики случайных величин

Конкретный вид функции распределения F(x), плотности распределения f(х) или перечисление значений р(х_i) для некоторого вариационного ряда называют законом распределения соответствующей случайной величины.

Хотя в природе существует бесконечное разнообразие случайных величин, законов распределения гораздо меньше.

Во-первых, различные случайные величины могут иметь совершенно одинаковые законы распределения. Например: пусть некоторая дискретная случайная величина y принимает всего два значения 1 и –1 с вероятностями 0,5. Тогда другая дискретная случайная величина z = –y имеет такой же закон распределения как и y.

Во-вторых, очень часто случайные величины имеют подобные законы распределения, отличающимися только одной или несколькими постоянными. Эти постоянные называются параметрами распределения.

Из всего многообразия законов распределения рассмотрим несколько наиболее типичных законов. Здесь важно обратить внимание на условия, при которых они реализуются, а также на параметры и свойства этих распределений.

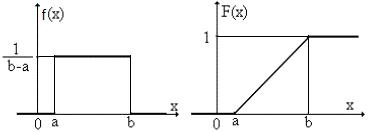Так называют распределение случайной величины, которая может принимать любые значения в интервале (a; b), причем вероятность попадания ее значения в любой отрезок, лежащий внутри интервала (a; b), пропорциональна только длине этого отрезка и не зависит от его положения внутри интервала.

Параметры распределения: a и b характеризуют только диапазон изменения значений случайной величины и больше ничего.

Примечание. Это распределение имеют самые "нехорошие" случайные величины, о которых практически ничего не известно (выпадение числа при бросании игральной кости или вращении рулетки).

2. Нормальное распределение N(m,σ)

Так называют распределение случайной величины, плотность распределения которой имеет вид:

f(х) = (2×π×σ)^–1/2×exp[–(x – m)²/2×σ²).

Параметры распределения: m и σ характеризуют соответственно наиболее вероятное значение случайной величины и степень ее рассеяния (дисперсию) относительно этого значения.

Примечание. Подавляющее большинство случайных величин окружающей природы имеют данное распределение – отсюда и его название (рост или вес людей).

Дата добавления: 2014-01-05