Линейная диаграмма

Описание сетевой модели в форме линейной диаграммы предполагает размещение работ в координатной системе, где по оси абсцисс (X) откладывается время (t), а по оси ординат (Y) – работы. Линейная диаграмма представляет собой особую форму изображения сетевой модели проекта, в которой каждая работа — отрезок, параллельный оси времени; длина этого от­резка равна продолжительности работы в выбранном масштабе. Если работе ничто не предшествует и она начинается в исходном событии, то она откладывается от начала временной шкалы, т.е. с самого левого края диаграммы. Точкой начала отсчета любой из других работ будет момент окончания всех предшествующих ей работ. События i и j на­чала и конца работы (i, j) ставят соответственно в начале и конце отрезка. Отрезки располагают один над другим, снизу вверх, в порядке возрастания индекса j, а для работ, входящих в одно и то же событие, — в порядке возрастания индекса i. Момент свершения исходного события считают рав­ным 0. Каждый отрезок размещают на диа­грамме таким образом, чтобы его начало сов­пало с самым правым концом всех отрезков, входящих в событие i. Иными словами, любое событие наступает только тогда, когда закончены все предшествующие ему работы. С другой стороны, оно является предпосылкой для начала следующих за ним работ. Событие не имеет продолжительности и наступает мгновенно. В связи с этим предъявляются особые требования к его определению.

Так, каждое событие, включаемое в сетевой график, должно быть полно, четко и всесторонне определено, его формулировка должна включать результат всех непосредственно предшествующих ему работ. И пока не выполнены все работы, непосредственно предшествующие данному событию, не может наступить и само событие, а, следовательно, не может быть начата ни одна из работ, непосредственно следующих за ним. Более того, если то или иное событие наступило, то это означает, что могут быть немедленно и реально начаты работы, следующие за ним. Если же по какой-либо причине хотя бы одна из таких работ не может быть начата, следовательно, нельзя считать данное событие наступившим.

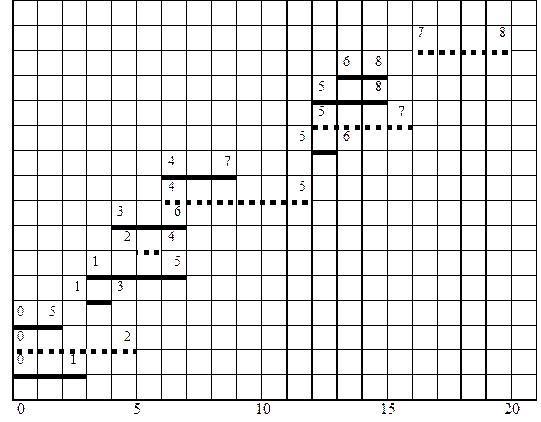
Рис. 3.2. Линейная диаграмма проекта

С помощью линейной диа­граммы можно определить критическое время, критические пути, резервы времени работ. Критическое время равно самой правой координате всех отрезков линейной диаграммы. Критический путь пред­ставляет собой цепочку отрезков — работ, соединяющих завершающее событие самой правой полоски с исходным. Этот путь выделен на рисунке пунктирной линией. Полный резерв времени работы равен максимальному сдвигу соответствующего отрезка вправо, который при этом не приведет к увеличению критического времени.

Дата добавления: 2014-01-05