Понятие устойчивости по Ляпунову

Пусть САУ описывается с помощью системы уравнений при заданных начальных условиях:

Решением данного уравнения является как функция начальных значений (уравнение невозмущенного движения). Здесь x_i⁰ – установившееся движение.

К системе приложено внешнее воздействие, которое привело к отклонению движения от установившегося

.

Для данных отклонений можно записать систему уравнений:

Уравнение - является уравнением возмущенного движения.

Невозмущенное движение () называется устойчивым по отношению к переменным x_i, если для любого положительного числа А², как бы мало оно ни было, найдется другое положительное число l², которое удовлетворяет условию для всех возмущений:

,

а возмущенное движение удовлетворяет условию

,

где m_i – весовые коэффициенты.

Движение будет устойчивым, если при небольших изменениях начальных условий, вызванных внешними воздействиями, невозмущенное движение будет отличаться от возмущенного движения мало.

Данное определение справедливо как для линейных, так и для нелинейных систем.

Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением

где - свободная составляющая выходной величины системы.

Система является устойчивой, если свободная составляющая x_c(t) переходного процесса с течением времени стремится к нулю, т.е. если

.

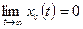Такая устойчивость называется асимптотической.

Если свободная составляющая неограниченно возрастает, т.е. если

,

то система неустойчива.

Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости.

Найдем общее условие, при котором система, описываемая уравнением (*), устойчива. Решение уравнения (*) равно сумме

где C_k – постоянные, зависящие от начальных условий; p_k – корни характеристического уравнения

.

Корни данного уравнения могут быть действительными (p_k=a_k), мнимыми (p_k=jb_k) и комплексными (p_k=a_k± jb_k).

Переходная составляющая (**) при t ®¥ стремится к нулю лишь в том случае, если каждое слагаемое вида . Характер этой функции времени зависит от вида корня p_k. Рассмотрим все возможные случаи расположения корней p_k на комплексной плоскости (см. рис.) и соответствующие им функции x_k(t), которые показаны внутри кругов (как на экране осциллографа).

1. Каждому действительному корню p_k=a_k в решении (**) соответствует слагаемое вида

Если a_k <0 (корень р₁), то функция (***) при t ®¥ стремится к нулю. Если a_k >0 (корень р₃), то функция (***) неограниченно возрастает. Если a_k =0 (корень р₂), то функция (***) остается постоянной.

2. Каждой паре сопряженных комплексных корней p_k=a_k± jb_k в решении (**) соответствуют два слагаемых, объединенных в одно

Эта функция представляет собой синусоиду с частотой b_k и амплитудой, изменяющейся во времени по экспоненте. Если действительная часть двух комплексных корней a_k <0 (корни р₄ и р₅), то колебательная составляющая (****) будет затухать. Если a_k >0 (корни р₈ и р₉), то амплитуда колебаний будет неограниченно возрастать. Наконец, если a_k =0 (корни р₆ и р₇), т.е. если оба сопряженных корня – мнимые (p_k=+ jb_k, p_k+1=- jb_k), то x_k(t) представляет собой незатухающую синусоиду с частотой b_k.

Общее условие устойчивости:

Для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательны.

При этом действительные корни рассматриваются как частный случай комплексных корней, у которых мнимая часть равна нулю. Если хотя бы один корень имеет положительную действительную часть, то система будет неустойчивой.

Устойчивость системы зависит только от вида корней характеристического уравнения и не зависит от характера внешних воздействий на систему. Устойчивость есть внутренне свойство системы, присущее ей вне зависимости от внешних условий.

Используя геометрическое представление корней на комплексной плоскости (см. рис.) в виде векторов или точек, можно дать вторую формулировку общего условия устойчивости (эквивалентную основной):

Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости. Если хотя бы один корень находится в правой полуплоскости, то система будет неустойчивой.

Мнимая ось jb является границей устойчивости в плоскости корней. Если характеристическое уравнение имеет одну пару чисто мнимых корней (p_k=+jb_k, p_k+1=-jb_k), а все остальные корни находятся в левой полуплоскости, то в системе устанавливаются незатухающие гармонические колебания с круговой частотой . В этом случае говорят, что система находится на колебательной границе устойчивости.

Точка b =0 на мнимой оси соответствует так называемому нулевому корню. Если уравнение имеет один нулевой корень, то система находится на апериодической границе устойчивости. Если таких корня два, то система неустойчива.

Дата добавления: 2014-01-05