Сложных электрических сетей

РАСЧЕТЫ УСТАНОВИВШИХСЯ РЕЖИМОВ

В практике электрических расчетов электрических систем и сетей расчеты установившихся режимов составляют значительную часть об­щего объема исследований, проводимых как на стадии проектировании электрических систем и сетей, так и на стадии их эксплуатации. Для какого бы типа электрических сетей ни проводились эти расчеты — системообразующих или распределительных — во всех случаях прихо­дится оперировать сложными схемами замещения, содержащими де­сятки, сотни и даже тысячи узлов и ветвей. Ясно, что в этих условиях не только решение, но и составление исходных уравнений установив­шегося режима электрической сети практически невозможно выпол­нять вручную. Поэтому расчеты установившихся режимов были одной из первых задач электроэнергетики, где нашли широкое применение электронные вычислительные машины (ЭВМ). Составление алгоритмов и программ расчета на ЭВМ потребовали разработки общих методов формирования и решения уравнений установившегося режима, не за­висящих от сложности и конфигурации схемы замещения электричес­кой сети и в то же время максимально учитывающих общие свойства, присущие различным конкретным электрическим сетям.

Формулировка общей задачи расчета установившегося режима электрической системы требует некоторых основных понятий и опре­делений.

Под установившимся режимом электрической системы понимается симметричный установившийся режим симметричной системы трехфаз­ного переменного тока. Схема замещения (расчетная схема) электри­ческой системы в этих условиях составляется на одну фазу с нейт­ралью (т.е. узлом, имеющим напряжение, равное нулю) и состоит из элементов электрической цепи: источников ЭДС и тока, активных сопротивлений, индуктивностей и емкостей.

Все элементы схемы замещения электрической системы можно разделить на активные и пассивные.

К активным относят элементы, генерирующие и потребляющие электроэнергию, т.е. генераторы электростанций и нагрузки подстан­ций. Как правило,, активные элементы в расчетах установившихся режимов представляются в виде источников тока, или "задающих токов". Представление в виде источников ЭДС используется крайне редко и далее рассматриваться не будет.

К пассивным относят элементы электрической системы, осуществ­ляющие передачу и преобразование электрической энергии, т.е. линии электропередачи, трансформаторы и автотрансформаторы, а также нерегулируемые статические устройства продольной и поперечной компенсации. Схемы замещения этих элементов состоят из активных, индуктивных и емкостных сопротивлений, образующих продольные (не связанные с нейтралью) или поперечные (связанные с нейтралью) ветви. В ряде случаев ветвь намагничивания схемы замещения транс­форматора или автотрансформатора вводится в расчеты постоянным отбором мощности, задаваемым, аналогично нагрузке, в виде источни­ка тока. Если схема замещения электрической системы не приводится к одной ступени напряжения, то в схемы замещения трансформатор­ных элементов вводятся кроме сопротивлений идеальные (без потерь) трансформаторы.

Параметры пассивных элементов схемы замещения электрической системы в расчетах установившихся режимов принимаются постоянны­ми, не зависящими от напряжений и токов этих элементов. В этом смысле говорят, что схема замещения электрической системы пред­ставляет собой линейную электрическую цепь, поскольку токи и напря­жения элементов этой цепи связаны соотношениями, образующими систему линейных алгебраических уравнений.

Расчет установившегося режима электрической системы заключает­ся в определении напряжений и токов, потоков активной и реактивной Мощности во всех ее элементах. В качестве исходных данных расчета задаются схема замещения электрической системы, значения парамет­ров пассивных элементов, а также значения параметров режима актив­ных элементов, определяемые реальными условиями работы источни­ков и потребителей электроэнергии в системе.

Источники электроэнергии (генераторы) вводятся в расчет постоянными значениями активной мощности (Р_Г = const) и модуля напряжения на зажимах (U_r = const), что определяется действием систем автоматического регулирования частоты и возбуждения. Кроме того, для одного из источников, называемого балансирующим, задается напряжение на шинах постоянное по модулю и фазе (U_r = const, 8_Г = const).

Нагрузки задаются статическими характеристиками активной и реактивной мощности по напряжению. Широко используемыми частными случаями такого представления являются задание нагрузок постоянной мощностью (Р_н = const, Qi = const) и постоянной проводимостью.

В ряде случаев могут применяться другие способы задания источ­ников и нагрузок. Так, например, если в результате расчета окажется, что значение реактивной мощности генератора недопустимо (Q_r < < Qr мин или Q_r > Q_r макс), то расчет режима следует повторить при фиксации реактивной мощности на соответствующем предельно допус­тимом значении, т.е. при задании генератора в виде Р_Г = const, Q_r = = const. Аналогично, если в результате расчета напряжение на шинах нагрузки окажется ниже минимально допустимого значения, то расчет может быть повторен при задании модуля напряжения и активной мощности нагрузки, с тем чтобы определить необходимую степень компенсации реактивной мощности нагрузки для обеспечения задан­ного допустимого уровня напряжения.

Указанное задание источников и потребителей электроэнергии соответствует введению их в расчеты нелинейными источниками тока, зависящими от напряжений. Таким образом, установившийся режим электрической системы математически описывается двумя группами уравнений: 1) линейными алгебраическими уравнениями, связы­вающими токи и напряжения пассивных элементов схемы замещения, представляющей собой линейную электрическую цепь; 2) нелинейны­ми уравнениями, связывающими мощности, напряжения и токи источ­ников и нагрузок.

Состояние линейной электрической цепи описывается уравнениями, составленными на основе первого и второго законов Кирхгофа и зако­на Ома. В расчетной практике широкое применение получили преоб­разованные — контурные и узловые — уравнения. Для электрической цепи переменного тока произвольной конфигурации, содержащей n узлов и m ветвей, система узловых уравнений имеет порядок (п — 1), а система контурных уравнений — порядок k = т — п + 1. При этом узловые уравнения приобретают наиболее простой вид при задании активных элементов электрической цепи только источни­ками тока, а контурные уравнения — при задании активных элементов только источниками ЭДС.

Схемы замещения

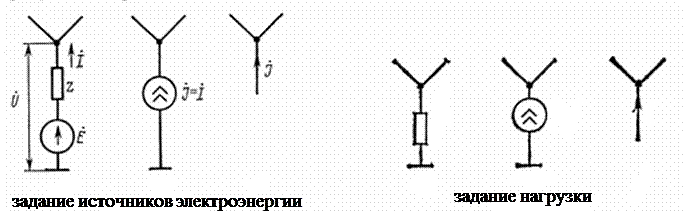
z – внутреннее сопротивление источника питания (ЭДС).

Нагрузка (потребители электроэнергии) задается либо в виде сопротивления либо в виде источника тока, равного взятому с обратным знаком току нагрузки, либо в виде задающего тока.

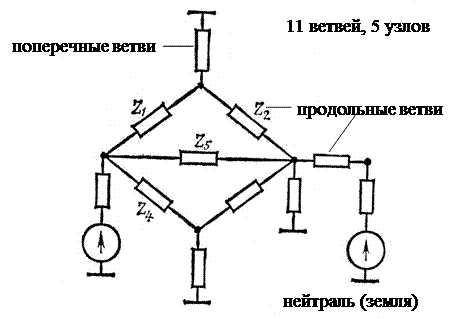
Ветви, связанные с узлом нейтрали (нагрузок и источников), называются поперечными. Другие – продольными.

1) обзываем узлы;

2) соответственно проставляем индексы сопротивлений, нагрузка и электростанции задаются в виде задающего тока.

Сопротивления не зависят от тока и напряжения – имеет место линейная электрическая цепь, которая описывается уравнениями законов Ома и Кирхгофа.

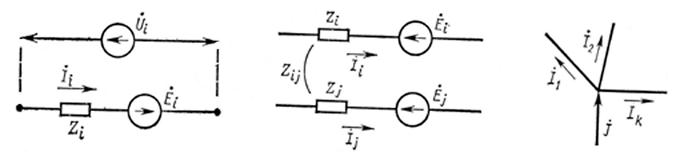Закон Ома для участка цепи с источником ЭДС:

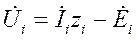(1).

В общем случае между отдельными ветвями i и j схемы замещения могут существовать взаимные сопротивления z_ij, обусловленные, например, взаимной индуктивностью. В схеме, обладающей свойством взаимности, взаимное сопротивление не зависит от очередности записи индексов: z_ij = z_ji.

Взаимное сопротивление определяет ЭДС 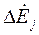, наведенную в ветви j током I_i, проходящим в ветви i, и наоборот:

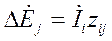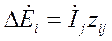и (2).

Таким образом, для ветвей, имеющих взаимное сопротивление, выражение (1) перепишется в виде:

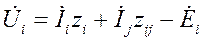и 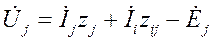при выбранных положительных направлениях.

Величины E_i и J_i (ЭДС источников и токи нагрузки) являются исходными (независимыми) параметрами режима, а величины z – параметрами системы. Знание этих величин необходимо для определения остальных (зависимых) параметров режима: токов и падений напряжения на ветвях.

Первый закон Кирхгофа определяет баланс токов в каждом узле электрической цепи: алгебраическая сумма токов в узле равна нулю. Для произвольного узла, содержащего источник тока J и связывающего k ветвей, уравнение первого закона Кирхгофа имеет вид (за положительное направление принимается направление тока к узлу): 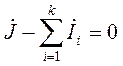(3).

Второй закон Кирхгофа определяет баланс напряжений в контурах электрической цепи и формулируется следующим образом: алгебраическая сумма падений напряжения на ветвях контура равна нулю.

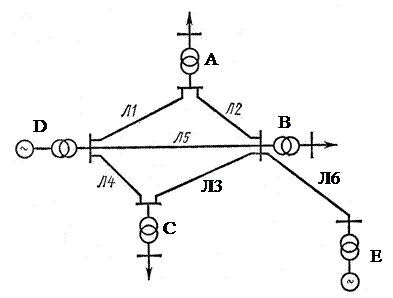
Составим уравнения состояния для схемы рис. 1, полагая, что в каждую ветвь дополнительно введен источник напряжения с ЭДС.

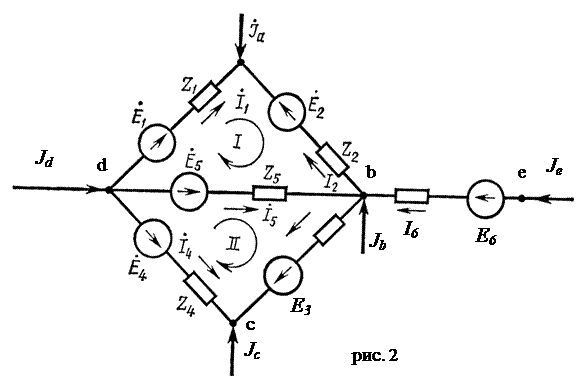
Уравнения первого закона Кирхгофа:

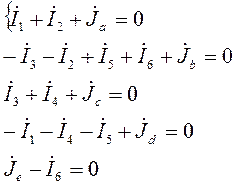(4)

Сумма этих уравнений приводит к тождеству: 0 = 0. Это обусловлено тем, что ток каждой ветви входит только в два уравнении (ветвь соединяет два узла), причем с противоположными знаками. Условие баланса требует, чтобы сумма токов источников энергии была равна сумме токов нагрузок. То есть, сумма задающих токов (источников напряжения и нагрузок) равна нулю:

.

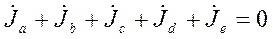Таким образом, уравнения (4) не являются взаимно независимыми: любое из них может быть получено в результате суммирования остальных.

Для электрической цепи, содержащей n узлов, можно составить (n-1) взаимно независимых уравнений вида (3), то есть один из узлов исключить из рассмотрения. Этот узел называется узлом баланса или балансирующим узлом.

Выберем в схеме рис. 2 узел d в качестве балансирующего. Это соответствует удалению из системы (4) четвертого уравнения. Тогда система перепишется в виде:

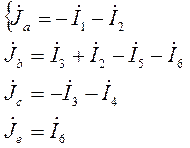(5)

Число неизвестных токов в уравнениях (5) равно числу ветвей (шести), то есть на два больше, чем число уравнений. Для получения двух недостающих воспользуемся вторым законом Кирхгофа (если направление обхода совпадает с направлением тока, то напряжение бреется со знаком "+"):

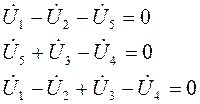(6)

Аналогично: нужно взять только два независимых контура, возьмем внутренние.

(7)

Используя уравнение закона Ома для участка цепи с ЭДС 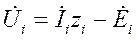, перепишем (7):

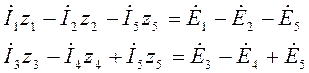(8)

Объединяя системы (5) и (8), получаем систему из шести независимых уравнений с шестью неизвестными токами (следовательно, система будет иметь единственное решение).

Схемы замещения современных сложных электрических систем содержат десятки и даже сотни узлов и ветвей. Количество уравне­ний состояния для таких систем соответственно настолько велико, что для их решения необходимо использовать цифровые электронные вычислительные машины (ЦВМ). Более того, составление уравнений состояния для сложных схем является весьма трудоемкой процеду­рой, и решение данной задачи также целесообразно возложить на ЦВМ. Для этого требуется иметь формализованный подход к состав­лению уравнений, который был бы одинаков для схем любой слож­ности и конфигурации. Такой подход может быть разработан на основе аналитического представления конфигурации схемы замещения с помощью элементов теории графов и алгебры матриц.

Дата добавления: 2014-01-05