КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
V.4. Расчет быстротоков
|
|
|
|
Гидравлический расчет. На оросительных и сбросных каналах ГЭС, проходящих по местности с большим уклоном, для преодоления больших разностей в отметках устраиваются специальные сооружения. Такими сооружениями являются или перепады (рис. V.7 а), создающие сосредоточенное падение дна в одном створе, или быстротоки (рис. V.7 6), с помощью которых разность отметок в дне канала распространяется на некоторую длину, зависящую от уклона быстротока. Гидравлический расчет сопряжения бьефов на перепадах делается так же, как и на плотинах; он был приведен в§V.2.
Быстроток представляет собой короткий лоток прямоугольного или трапецеидального сечения с большим уклоном дна (i от 0,10 до 0,25).
Ширину быстротока делают или постоянной, или переменной с сужением вниз по течению.

Рис. V.7.


По длине быстротока, в зависимости от типа входной части, устанавливается обычно кривая спада типа 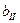 и реже кривая подпора типа
и реже кривая подпора типа  .
.
В начале быстротока с горизонтальным дном или малым уклоном устанавливается критическая глубина  , от которой пойдет кривая спада до бытовой глубины h0 <
, от которой пойдет кривая спада до бытовой глубины h0 < , соответствующей уклону быстротока
, соответствующей уклону быстротока  >
> 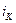 .
.
Если входная часть быстротока осуществляется в виде порога, то ниже порога устанавливается сжатая глубина hc. Если hc > h0, то на быстротоке устанавливается кривая спада, если же hc < h0, то на быстротоке будет кривая подпора типа  от глубины hc до h0.
от глубины hc до h0.
В определении этих глубин и построении формы кривой свободной поверхности по длине быстротока и заключается гидравлический расчет быстротока.
Устройство быстротоков с сужением ширины по длине имеет целью уничтожение кривой спада по длине быстротока и получение постоянной глубины без увеличения скоростей.
При сопряжении быстротока с каналом устраивают успокоитель, имеющий назначение гасить энергию потока и создавать такие условия сопряжения, при которых не происходило бы размывов в отводящем канале. Успокоитель устраивают обычно в виде водобойного колодца с постепенно расширяющимся переходным участком канала. Гидравлический расчет успокоителя делается так же, как и водобойного колодца (см.§ V.3).
Пример 3. На канале трапецеидального сечения с шириной 6 = 10 м, 1=0,0003, m=l,5, n = 0,017, Q=40 м3/сек устроен быстроток с уклоном i = 0,10, длиной 120 м. Требуется построить кривую спада по длине быстротока.
Решение. Определяем критическую глубину для расхода Q = =40 м3/с (см. § 6.7).
Для прямоугольного сечения с шириной по дну 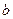 = 10 м и Q = =40 м3/сек.
= 10 м и Q = =40 м3/сек.
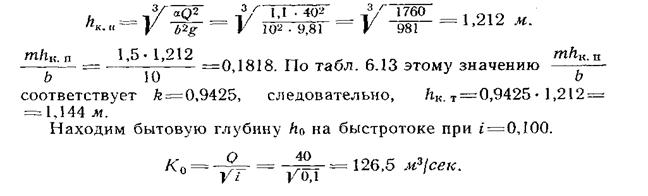
Таблица V.2.
|
|

|

При истечении из отверстия струя жидкости претерпевает значительные изменения. Это происходит из-за непараллельности движения струек в сечении отверстия, что обусловливает уменьшение площади поперечного сечения струи на выходе отверстия на расстоянии 0,5 d от внутренней стенки сосуда (рис. VI. 1,а). Это сечение называется сжатым. Движение струи в сжатом сечении близко к параллельно-струйному.
Площадь сжатого сечения струи  несколько меньше площади отверстия ω. Отношение площади сжатого сечения струи
несколько меньше площади отверстия ω. Отношение площади сжатого сечения струи  к площади отверстия называется коэффициентом сжатия струи
к площади отверстия называется коэффициентом сжатия струи  .
.
Далее струя падает под действием силы тяжести, и поперечное сечение струи изменяет свою форму. Это явление носит название инверсии струи. Так, при истечении из круглого отверстия поперечное сечение струи принимает форму эллипса, при истечении из треугольного отверстия — форму треугольной звезды.
Сжатие струи зависит от расположения отверстия относительно боковых стенок сосуда. В зависимости от этого различают полное и неполное, совершенное и несовершенное сжатие.
Если струя имеет сжатие по всему периметру, то сжатие называется полным. Неполное сжатие будет иметь место в том случае, если струя не испытывает сжатия по одной или же по нескольким сторонам. Неполное сжатие будет у отверстия, расположенного около боковой стенки резервуара. Коэффициент сжатия  будет иметь большее значение при неполном сжатии.
будет иметь большее значение при неполном сжатии.
Полное сжатие струи разделяется на совершенное и несовершенное. Сжатие называется совмещенным, если отверстие расположено достаточно далеко от боковых стенок, свободной поверхности и дна, и они не оказывают влияния на характер истечения. Совершенное сжатие наблюдается, когда расстояние от стенок до отверстия превышает утроенный соответствующий размер отверстия. Для круглого отверстия это расстояние должно быть не менее трех диаметров отверстия, для прямоугольного отверстия, (рис. VI. 1, б) условиями совершенного сжатия будут 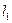 > 3 а и
> 3 а и  > 3
> 3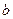 .
.
Если это условие не соблюдается и отверстие находится на бо-
лее близком расстоянии от стенок, то сжатие называют несовер-
шенным. При несовершенном сжатии коэффициент ε будет больше,
чем при совершенном.
При истечений из отверстий задача сводится к определению скорости и расхода вытекающей жидкости. Рассмотрим истечение жидкости через малое отверстие в тонкой, боковой стенке (рис. VI. 1, а) при постоянном напоре Н. Выберем два сечения: 1–1 — на свободной поверхности жидкости в резервуаре, 2—2 — в сжатом сечении струи. Плоскость сравнения О – О проведем по

|



















ГЛАВА VII. НАПОРНЫЕ ТРУБОПРОВОДЫ
Строитель транспортных сооружений часто в своей инженерной практике сталкивается с устройствами и системами, работающими в напорном режиме, полным сечением. Наиболее распространенные из них — длинные и короткие трубопроводы, насадки, отверстия. В этой главе дается их классификация на основе гидравлических особенностей указанных устройств. Данные особенности определяют специфику расчетных зависимостей и методику их применения, базирующихся на законах гидравлики.
§ VII. 1. Классификация напорных систем
Напорные системы классифицируют по соотношению местных потерь энергии и потерь по длине. Необходимость учета того или иного вида сопротивлений лежит и в основе частных методик расчета.
|

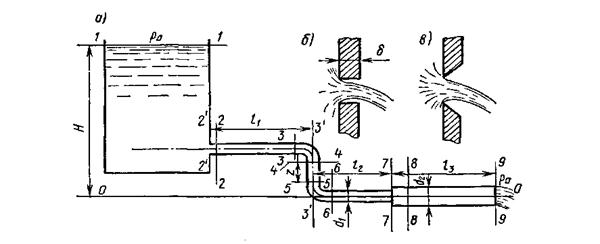
Рис. VII.1

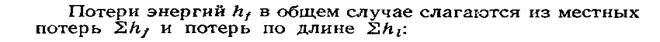


Участки резкоизменяющегося движения в местах расположения местных сопротивлений (входы, повороты, расширения и др.) часто имеют пренебрежимо малую протяженность по сравнению с длиной участков плавноизменяю-щегося движения. Поэтому можно считать длину l1 равной расстоянию между сечениями 2' и 3', 12 — расстоянию между сечениями 3' и 7 и т. д.
Придерживаясь указанного в начале принципа классификации, системы, у которых в общей сумме местные потери энергии пренебрежимо малы ( <<
<<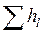 ), называют трубопроводами.
), называют трубопроводами.
Системы, в которых местные потери энергии и потери на трение по длине соизмеримы ( ≈
≈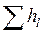 ), называются короткими трубами. Короткие патрубки, в которых местные потери значительно превосходят потери по длине, называются насадками.
), называются короткими трубами. Короткие патрубки, в которых местные потери значительно превосходят потери по длине, называются насадками.
Если длина насадка настолько мала, что не влияет на характер течения, то такие системы относят к отверстиям в тонкой стенке (рис. VII.1, б).Здесь толщина δ, которую можно считать как длину насадка, настолько мала, что оторвавшаяся от стенок при входе в отверстие струя нигде не касается поверхности отверстия на всей толщине стенки. Поэтому такая толщина стенок или подобная длина насадка не могут повлиять на характер течения. Оно будет таким же, как у отверстия с острыми кромками (рис. VII.1, в).
Примером трубопроводов могут быть водопроводные линии, имеющие при значительной протяженности относительно малое количество регулирующих, запорных и других устройств. На городских линиях длиной свыше 200 м при диаметре до 200—500 мм местные потери энергии не превышают 3—5% от потерь по длине. В то же время линии такой же длины, предназначенные для подачи сырья и продукции, например на нефтехимических заводах, как правило, насыщены местными сопротивлениями значительно выше. Их вклад в общий баланс потерь энергии становится ощутимым, что позволяет отнести указанные системы к коротким трубам.
В дорожном строительстве типичный случай коротких труб — напорные водопропускные трубы, уложенные под насыпью дорог (рис. VII.2, слева). В методике их расчета широко используются сведения и о работе насадков. В то же время дорожные трубы могут работать и по принципу истечения через отверстия в тонкой стенке (рис. VII.2, справа).
|

Насадки и отверстия широко применяются в технике. К ним относятся, например, жиклеры и форсунки двигателей, наконечники гидромониторов и брандспойтов и т. д.
Коэффициенты сопротивления и скорости системы. Потери энергии в общем случае определяются по формуле Вейсбаха (4.10). Выражение потерь энергии по этой формуле в общем случае приведет к появлению в исходном уравнении (VII.1) в качестве аргументов нескольких скоростей. Например, в выражения потери энергии на вход или по длине 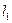 (см. рис. VII.1, а) будет входить скорость ν2, соответствующая диаметру
(см. рис. VII.1, а) будет входить скорость ν2, соответствующая диаметру 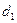 :
:
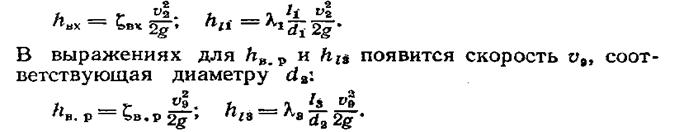
Уравнение неразрывности дает возможность все скорости, входящие в формулу (VII.2) потерь энергии при использовании формулы Вейсбаха (4.10), свести к одной из них, например к уже имеющейся в уравнении (VII.1) скорости υ9:
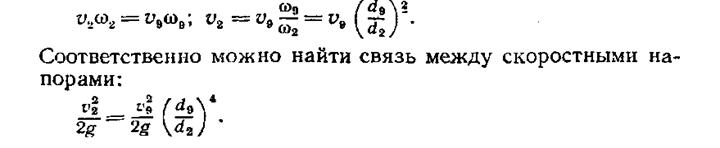
Выражения такого типа дают возможность свести исходное уравнение Бернулли к функции скорости в одном сечении (в рассматриваемом примере — к скорости υ9). При этом для потери энергии получаем выражения вида
 | |||||
| |||||
|
Коэффициенты сопротивления, приведенные к скорости в одном сечении, отмечены штрихом
|
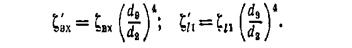
Теперь выражения потерь энергии (5.2) тоже приводятся к одной скорости;
 |
Сумма коэффициентов Σζ, приведенных к одной скорости, называется коэффициентом сопротивления системы. Подстановка выражения (VII.6) в исходное уравнение (VII.1) дает возможность найти выражение скорости υ9 , а следовательно, и расхода:
 |
|
 |
Рис.VII.3.
В этом трубопроводе вдоль линии уменьшаются диаметры d1 > d 2> d 3 труб и часть общего расхода Qзабирается в узлах: q1 q2. Все остальные схемы трубопроводов относятся к сложным трубопроводам, когда есть разветвления и параллельные линии. Примером сложного трубопровода является схема на рис. VII.3, б.Она похожа на представленную на рис. VII.3, а,но на ней добавлены линии 1 и 2,обеспечивающие отвод расходов qx и q2.Схема на рис. VII.3, бпредставляет собой частный случай сложного трубопровода — тупиковую систему, в которой каждое ответвление заканчивается тупиком. Другой тип сложного трубопровода — кольцевая система характерен тем, что к узлам жидкость может быть подана, по крайней мере, по двум линиям, а отдельные линии образуют замкнутые контуры — кольца (ABCDAна рис. VII.7.3, в).Тупиковые системы более дешевы, чем кольцевые, но последние — надежнее.
§ VII.2. Простой трубопровод
Сопоставление простых и сложных трубопроводов на рис. VII.3 приводит к выводу, что любая из этих систем может быть разделена на ряд простых трубопроводов. Поэтому естественно, что методика расчета простых трубопроводов является основой для решения задач сложных систем. Для простого трубопровода (рис. VII.3, а ) как системы последовательно соединенных участков труб со значительным преобладанием потерь энергии на трение по сравнению с местными потерями позволяет записать уравнение Бернулли для начального сечения по свободной поверхности жидкости в резервуаре и на выходе (в конце участка  3) как
3) как
|

Зависимость (VII.10) называется уравнением проостого трубопровода. В общем случае действующий напор Н — не только перепад геометрических высот системы. Он может включать разность удельных работ сил давления в начальном и конечном сечениях, если давления в них не уравновешивают друг друга.
|
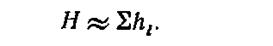
Зависимость (5.11) весьма показательна: в простом трубопроводе вся исходная энергия напора Н идет практически только на преодоление сопротивления по длине. Для замкнутых кольцевых линий выражение (VII.11) является не приближенным, а точным. Это следует из уравнения Бернулли.
Если движение в системе установившееся, то в общем случае на участках, где диаметр, расход и шероховатость одинаковы, его можно считать и равномерным. При этом потери энергии на трение по длине можно рассчитывать по формуле Дарси — Вейсбаха, но наиболее просто это сделать по формуле Шези  , где
, где  –расходная характеристика (модуль расхода). Современная технология изготовления позволяет получить практически постоянную шероховатость поверхностей труб из заданного материала и данного диаметра. Благодаря этому были составлены таблицы расходных характеристик К (
–расходная характеристика (модуль расхода). Современная технология изготовления позволяет получить практически постоянную шероховатость поверхностей труб из заданного материала и данного диаметра. Благодаря этому были составлены таблицы расходных характеристик К (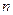 ; d) для принятого сортамента при квадратичном законе сопротивления [15, 18]. Примеры даны в табл. VII.1, VII.1
; d) для принятого сортамента при квадратичном законе сопротивления [15, 18]. Примеры даны в табл. VII.1, VII.1
С учетом формулы (VII.11) уравнение простого трубопровода приводится к виду
|
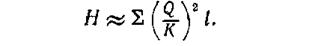
Таблица VII.1. Модуль расхода К для чугунных труб различных
диаметров, работающих в зоне квадратичного сопротивления
|
|
|
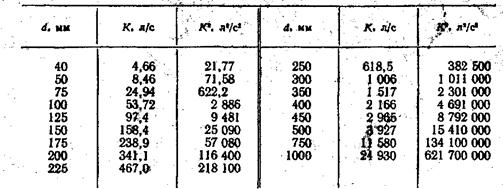
Таблица VII.2. Модуль расхода К для абсолютной шероховатости
 = 0.2, 0.5, и 1.0 мм
= 0.2, 0.5, и 1.0 мм

Методика расчета на основе формулы (VII.12) может быть использована и для других характерных случаев сопротивления: для переходной области и гладких поверхностей. При этом в расходные характеристики зоны квадратичного сопротивления вносят имеющиеся в справочниках [15, 21] поправки (обычно в функции чисел Рейнольдса).
|

§ VII.3. Сложные трубопроводы
Сложные трубопроводы отличаются большим разнообразием, поэтому для них отсутствует единое математическое описание. Применительно к сложным системам можно говорить только о принципах расчета, демонстрируя их примерами.
Как уже говорилось, каждый сложный трубопровод можно представить как ряд простых, например линии 1 и 2 в тупиковой системе на рис. VII.3, б. В основе решения сложных систем лежат два основных уравнения гидравлики: Бернулли и неразрывности. Причем для составляющих сложную систему простых трубопроводов уравнение Бернулли обычно применяется в форме уравнения простого трубопровода.
Следовательно, первый принцип решения сложных трубопроводов можно сформулировать так: для описания сложной системы на базе уравнения Бернулли можно составить столько уравнений, сколько простых трубопроводов образуют эту систему.
Уравнение неразрывности применительно к узлам системы (местам соединения отдельных линий) записывается в форме
 (VII.14)
(VII.14)
Это равенство подразумевает, что «положительные» расходы  отдельных линий, по которым жидкость подходит к рассматриваемому узлу, компенсируются «отрицательными» расходами в тех линиях, по которым происходит отток от узла. К последним относится в общем случае и расход, потребляемый непосредственно в узле. Отсюда вытекает второй принцип расчета сложных трубопроводов: на основе уравнения неразрывности для описания сложной системы можно составить столько уравнений, сколько узлов входит в систему.
отдельных линий, по которым жидкость подходит к рассматриваемому узлу, компенсируются «отрицательными» расходами в тех линиях, по которым происходит отток от узла. К последним относится в общем случае и расход, потребляемый непосредственно в узле. Отсюда вытекает второй принцип расчета сложных трубопроводов: на основе уравнения неразрывности для описания сложной системы можно составить столько уравнений, сколько узлов входит в систему.
Сформулированные принципы позволяют составить систему уравнений, описывающих течение жидкости в сложном трубопроводе в предположении равномерного движения на каждом его участке между соседними узлами. Для кольцевых систем первый принцип может иметь частный вид. Составим уравнение Бернулли для кольца, например ABCDA (рис. VII.3, в). От сечения 1—1 будем совершать обход кольца по часовой стрелке, замкнув его в том же сечении.
На участке АВ длиной l1 направление обхода кольца и движения жидкости, показанное на рис. VII.3, в стрелками, совпадают — на этом участке получаем положительный перепад энергий 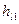 между узлами А и В. На участке BCDА длиной 12 направления обхода и течения жидкости противоположны. Получаем отрицательный перепад энергий
между узлами А и В. На участке BCDА длиной 12 направления обхода и течения жидкости противоположны. Получаем отрицательный перепад энергий 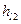 между теми же узлами В и А.
между теми же узлами В и А.
При совмещении начального и конечного сечений 1—1 получаем из уравнения Бернулли Σ =0, т. е. алгебраическая сумма потерь энергии по любому кольцу равна нулю. Согласно этому уравнению для кольца имеем
=0, т. е. алгебраическая сумма потерь энергии по любому кольцу равна нулю. Согласно этому уравнению для кольца имеем 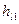 =
=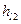 или, обобщая, потери энергии во всех параллельных линиях равны.
или, обобщая, потери энергии во всех параллельных линиях равны.
Более наглядно полученный результат можно объяснить так. Из узла Авыходит несколько единиц веса жидкости. Согласно уравнению Бернулли, их энергия одинакова
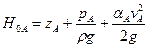 .
.
Часть жидкости идет по линии l1, часть — по линии 12(в общем случае — по 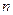 линии). Но при объединении параллельных линий в узле Ввсе части согласно уравнению Бернулли должны иметь снова одинаковую удельную энергию:
линии). Но при объединении параллельных линий в узле Ввсе части согласно уравнению Бернулли должны иметь снова одинаковую удельную энергию:
 .
.
Следовательно, потери энергии во всех параллельных линиях равны, а скорости выше в тех из них, где меньше сопротивление.
В заключение следует отметить, что зависимость Σ =0 позволяет составить для кольцевого сложного трубопровода столько уравнений, сколько в системе колец. В целом, для кольцевой сети на основе сформулированных выше принципов может быть составлена замкнутая система уравнений.
=0 позволяет составить для кольцевого сложного трубопровода столько уравнений, сколько в системе колец. В целом, для кольцевой сети на основе сформулированных выше принципов может быть составлена замкнутая система уравнений.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 5243; Нарушение авторских прав?; Мы поможем в написании вашей работы!

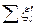 и местных
и местных 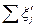 сопротивлений, если
сопротивлений, если