Гравитационная, или грунтовая, вода заполняет все поры грунта и нахо­дится под действием силы тяжести

Рис. VIII.1. Рис. VIII.2.

Заполняющая поры грунта гравитационная вода, находясь в состоянии движения, образует горизонт грунтовой воды или фильтрационный по­ток. Следует отметить, что в связных грунтах капиллярный слой воды бывает довольно значительным, и гидравлические решения, основанные на законах дви­жения только гравитационной воды, бывают не совсем точными.

Движение грунтовых вод может быть напорным (рис. VIII.1) и безнапорным (рис. VIII.2). При безнапорном движении в грунтовом потоке имеется свободная поверхность.

Некоторые вопросы фильтрации достаточно просто и точно решаются гидрав­лическим путем. Другие же вопросы фильтрации разрешаются лишь методами гидромеханики, основанными на применении точного математического анализа.

VIII. 2. Основной закон фильтрации

Основной закон фильтрации, называемый законом Дарси, был установлен в 1852—1855 гг. на основе опытов, проведенных с песчаным грунтом.

Опытная установка для демонстрации этого закона состоит (рис. VIII.3) из вертикального цилиндра, в боковой стенке которого поставлен ряд пьезометров.

Цилиндр заполнен испытуемым грунтом, лежа­щим на специальной сетке. Над грунтом поддер­живается постоянный уровень воды, притекающей через кран; излишек воды свыше определенного уровня сливается через трубу.

Фильтрующаяся через грунт вода собирается под решеткой на дне цилиндра и вытекает наружу через кран.

После регулировки подачи воды краном доби­ваются равенства притока и фильтрации воды через грунт в цилиндре, при котором движение грунтовой воды будет установившимся.

Выбрав по высоте цилиндра два сечения на расстоянии , можно будет наблюдать различные уровни воды в пьезометрах 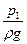и 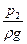, разность которых (рис. VIII.3) 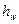показывает потерю напора на длине .

Предположив, что в однородном грунте потери напора по длине происходят равномерно, можем найти гидравлический уклон , представляющий потерю на­пора на единицу длины:

Рис. VIII.3.

Если обозначить сечение цилиндра через ω, то фильтрационный расход че­рез грунт будет

где 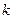— коэффициент фильтрации.

Частное от деления расхода Q на всю площадь сечения ω

(VIII.2)

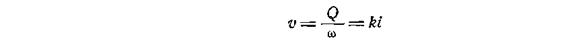
называется скоростью фильтрации.

Как видим из выражения (VIII.2), скорость фильтрации пропорциональна ко­эффициенту фильтрации 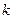и первой степени уклона (это и есть так называемый закон Дарси), последнее объясняется тем, что движение грунтовых вод происходит при ламинарном режиме.

Скорость фильтрации есть фиктивная скорость, так как при определении ее мы брали полную площадь сечения ω вместе с площадью твердых частиц.

В дей­ствительности, если площадь пор в сечении обозначить 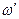, то средняя скорость

(VIII.3)  

Акад. Η. Н. Павловский на основе опытных данных установил величину кри­тической скорости фильтрации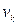, для которой применим закон Дарси

(VIII.4)  

где ρ — коэффициент порозности, 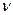— кинематический коэффициент вязкости в см²/сек, 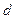— диаметр зерен грунта в см; N — постоянное число, равное 50—60.

При 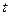=10° и v=0,013 р=0,40 (среднее значение порозности в песчаных грун­тах) и N =50 формула (VIII.4) приобретает вид

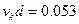(VIII.5)

При скорости фильтрации 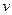>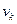движение грунтовых вод подчиняется урав­нению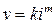, где m — показатель степени, приближающийся к 0,5, как при турбу­лентном движении подземных вод.

В этом случае для определения скорости турбулентной фильтрации акад. Η. Н. Павловский предложил формулу, аналогичную формуле Шези:

где А — эмпирический коэффициент, определяемый для крупнозернистых грунтов (d>5 см) по формуле С. В. Избаша

§ VIII.3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ФИЛЬТРАЦИИ

		Коэффициент фильтрации , характеризующий водопроницаемость грунта, за­висит от многих факторов: величины и формы частиц грунта, степени их однород­ности и от температуры воды. Распределение различных частиц данного грунта по крупности обычно характеризуется грануло­метрической кривой, получаемой в резуль­тате механического анализа грунта. На оси абсцисс этой кривой (рис. VIII.4) откладыва­ются значения диаметра частиц, а на оси ординат — процентное отношение суммар­ного веса частиц с диаметром меньше дан­ного к весу всего исследуемого образца грунта. Коэффициент фильтрации можно оп­ределить одним из следующих способов:

Рис. VIII.4  

VIII.4

· с помощью специальных формул, в которые входят физические постоянные грунта;

· лабораторным исследованием образ­цов грунта в специальных приборах;

· в ответственных случаях, для круп­ных проектов, коэффициент фильтрации оп­ределяется изучением грунта в полевых условиях с помощью пробных откачек воды из колодцев или нагнетаний.

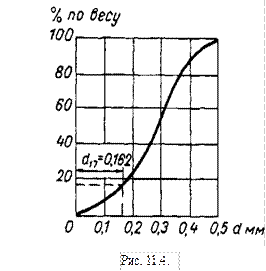
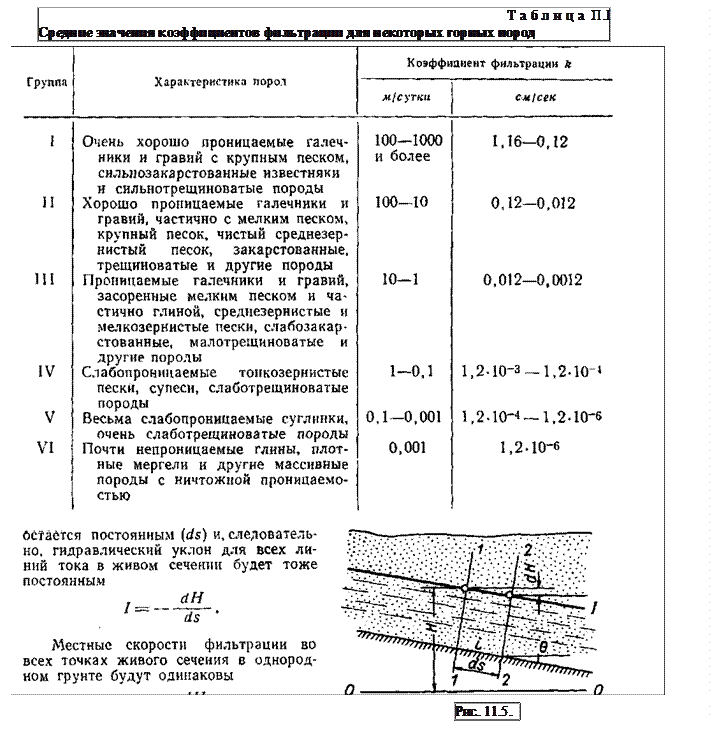
В табл. 11.1 приведены средние значения коэффициента фильтрации для не­которых грунтов.

§ VIII.4. УРАВНЕНИЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД

Пусть имеется грунтовой поток с плавно изменяющимся движением; выделим в грунтовом потоке (рис. VIII..5) два живых сечения, находящихся на расстоянии ds друг от друга. При плавно изменяющемся движении давление в живом сечении распределяется по законам гидростатики и удовлетворяет закону

Рис. VIII.5.  

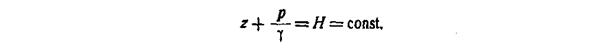
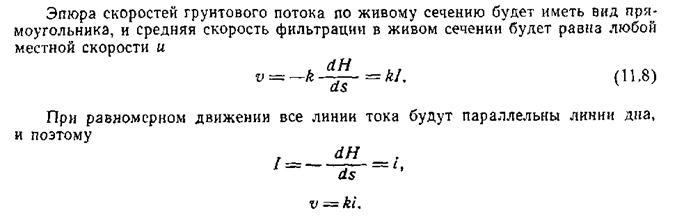
При неплавно изменяющемся движении грунтового потока уравнение (VIII.8) не будет справедливо, так как линии тока значительно искривлены, гидравличе­ский уклон и местные скорости и будут различными по живому сечению, и рас­чет движения грунтового потока получается много сложнее.

Рассмотрим грунтовой поток с плавно изменяющимся движени

	Рис. VIII.6. Рис. VIII.7.

Рассмотрим грунтовой поток с плавно изменяющимся движением (рис. VIII.6). Для него, согласно уравнению (VIII.2), v=ki. Возьмем в потоке два сечения 1 — 1 и 2 — 2 с координатой свободной поверхности ζ и глубиной потока h в се­чении 1— 1. Обозначим уклон водонепроницаемого слоя i, а уклон свободной по­верхности I. Тогда

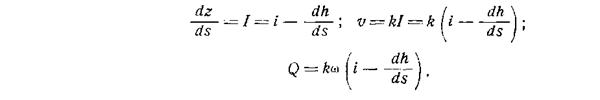
Полученное выражение является основным уравнением неравномерного дви­жения грунтового потока.

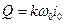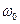Если бы движение грунтового потока было равномерным, то расход был бы , где и 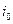— площадь живого сечения и уклон грунтового потока при равномерном движении.

§ VIII.4. РАСЧЕТ ДЕБИТА (РАСХОДА ВОДЫ) СКВАЖИНЫ ИЛИ КОЛОДЦА ПРИ ОТКАЧКЕ

Рассмотрим откачку воды из колодца или скважины, заложенной в водоносном пласте с горизонтальным непрони­цаемым подстилающим слоем. До начала откачки грунтовые воды в пласте находятся в покое и поверхность их горизон­тальна. Если начать откачку воды из скважины, в водоносном слое начнётся движение грунтовых вод. При этом уровень воды в скважине понизится. Одновременно произой­дёт понижение уровня грунтовых вод в пласте; это пониже­ние будет наибольшим у стенок скважины, постепенно убывая по мере отдаления от нее (рис. VIII.8.). Чем интенсивнее будет производиться откачка, тем ниже будет располагаться уровень воды в скважине и тем больше будет ее дебит (расход).

Уровень стояния воды в скважине до начала откачки Н_ст, одинаковый с уровнем во всём водоносном пласте, обычно называют статическим. Уровень H_д устанавливающийся в скважине в процессе откачки, носит название динамического, а сечение открытой поверхности уровня воды в пласте вер­тикальной плоскостью, проходящей через ось колодца, называется кри­вой депрессии, или кри­вой падения уровня (схе­матически показана пунк­тиром на рис.).

Рис. VIII.8. Кривая депрессии при откачке грунтовых вод

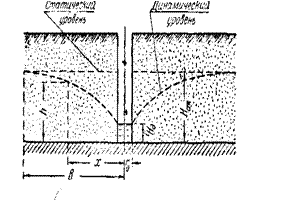
При откачке из одиночной скважины сниже­ние уровня, вызываемое откачкой, на некотором расстоянии от оси скважины практически перестаёт быть заметным; это расстояние называется радиусом дренирования, или радиусом влияния колодца (скважины). При предварительных расчётах его можно принимать равным для песчаных грунтов от 350 до 500 м, для крупнозернистых грунтов — 700 м. Радиус влияния можно определить по эмпирической формуле И.П. Кусакина , где – глубина откачки 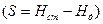, 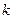– коэффициент фильтрации (м/сек). Предполагая величину этого радиуса R известной, зная толщину (мощность) водоносного слоя и задаваясь динами­ческим уровнем в колодце (скважине), можно определить расход воды в колодце и установить приближённую форму кривой депрессии.

Для этого рассмотрим движение воды через некоторое цилин­дрическое сечение водоносного слоя на расстоянии x от оси ко­лодца. Если глубина воды в этом сечении площадь сечения будет равна F=2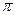xh. При этом расход фильтрации где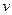– скорость фильтрации, определяемая, как обычно, по фор­муле Дарси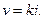

Подставляя это значение скорости в выражение для расхода, по­лучим: Гидравлический уклон в этом выражении можно заменить через отношение бесконечно малой потери напора, т. е. падения уровня dh, к бесконечно малому пути в радиальном направлении dx: 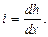Тогда 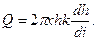Интегрируя это уравнение в пределах: для х от (радиус колодца) до и соответственно для от H_д до Н_ст , получим искомый дебит (расход воды) колодца или скважины в виде

Из дифференциального уравнения (1) можно получить уравнение для кривой депрессии: Откуда 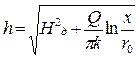(см. обозначения на рис. VIII.8).

Рассмотрим случай артезианских вод, когда водоносный пласт располагается между двумя водонепроницаемыми слоями и находится под избыточным давлением (рис. VIII.9).

Если в таком пласте заложить колодец (скважину) и про­изводить из него откачку воды, то толщина водоносного слоя изменяться не будет, а вместо этого будет изме­няться давление в пласте, убывая по направлению к колодцу. Отметим, что в тех случаях, когда глубина колодца меньше напора, соответствующего давлению в пласте до начала откачки, колодец будет фонтанировать и вода самоизливаться на поверхность земли. Подобного рода колодцы (скважины) обычно называются артезианскими.

Рис. VIII.9.

Выводы, аналогичные приведенным выше, позволяют получить следующее уравнение для дебита артезианской скважины (см. обозначения на рис. VIII.9):

§ VIII.5. ФИЛЬТРАЦИЯ ВОДЫ ЧЕРЕЗ ЗЕМЛЯНУЮ ПЛОТИНУ.

Рассмотрим пло­тину, образованную однородным грунтом в отношении коэффи­циента фильтрации, расположенную на горизонтальном водоне­проницаемом оснований (рис. VI 1.4). Картина фильтрации череа такую плотину имеет вид^ представленный линиями токов, которые начинаются на верховом откосе А В и заканчиваются на низовом откосе CD. Самая верхняя линия тока be является кривой депрес­сии. Она характеризуется тем, что давление во всех ее точках оди­наково и равно атмосферному давлению. Выход этой линии на ни­зовой откос называется точкой высачивания (точка с).

Гидравлический расчет земляной плотины сводится к определе­нию фильтрационного расхода, проходящего через тело плотины,, и к построению кривой депрессии, необходимой при проектирова­нии плотины.

Для упрощения расчета земляной плотины рядом авторов (Е. А. Замариным, Η. Н. Павловским, А. А. Угинчусом, Шаффер-наком и др.) было предложено заменять трапецеи-

		Рис. VIII.4. Поперечное сечение земляной плотины

ПРИЛОЖЕНИЕ 1

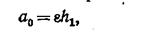
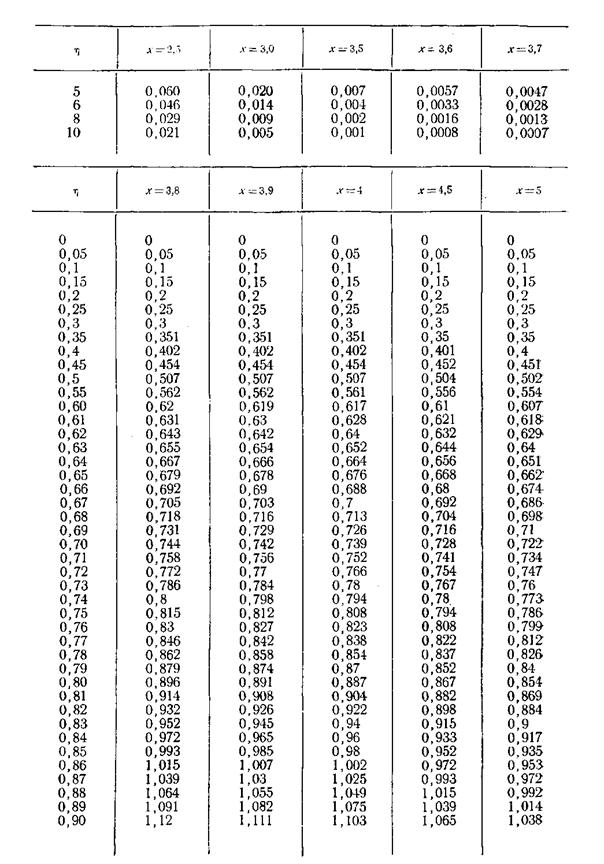
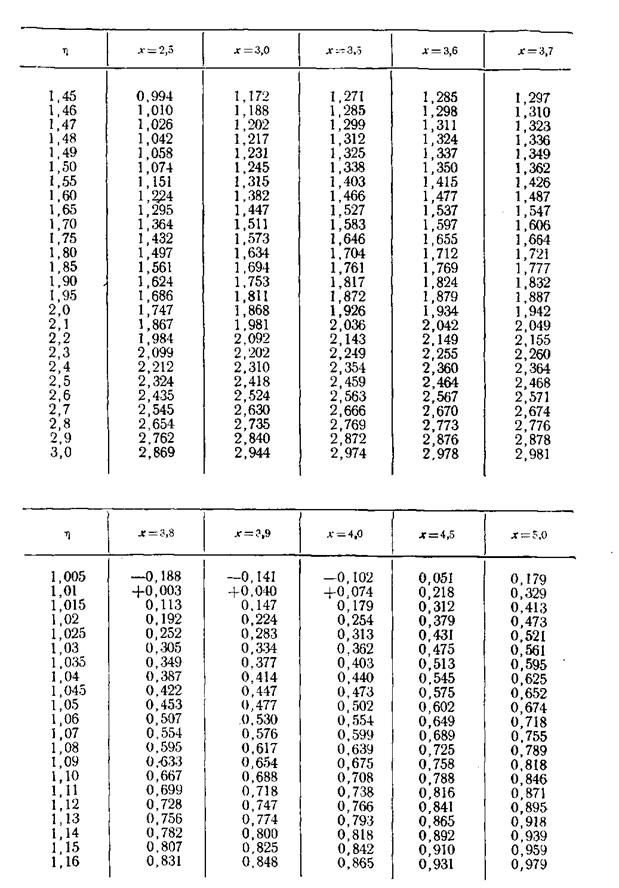
ПРИЛОЖЕНИЕ 2

Дата добавления: 2014-01-05