Метрические задачи. Ортогональная проекция прямого угла

К метрическим задачам, изучаемым в учебном курсе начертательной геометрии, относятся задачи, в которых требуется определить метрические характеристики заданной фигуры – длину, угол, площадь и другие, а также метрические свойства и характеристики, обусловленные расположением фигуры относительно плоскостей проекций или относительно другой (других) фигур – перпендикулярность, расстояние и угол. Проекционное решение таких задач основывается на метрических свойствах ортогонального проецирования на плоскость и обратимости чертежа Монжа. Метрическими свойствами ортогонального проецирования являются существующие зависимости между длинами отрезка прямой линии и его проекции, а также между величинами угла и его проекции (см. п. 1). Из этих зависимостей вытекает теорема о проецировании прямого угла: для того чтобы прямой угол проецировался в прямой угол, необходимо и достаточно, чтобы одна его сторона была параллельна плоскости проекций, а другая неперпендикулярна этой плоскости. Рассмотрим геометрическое доказательство. Оно позволяет более наглядно увидеть числовую и проекционную взаимосвязь двух геометрических фигур – прямого угла и его проекции.

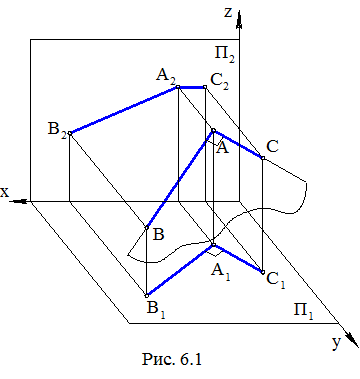
Необходимость. Пусть ÐBAC = = ÐB₁A₁C₁ = 90° (рис. 6.1). Докажем, что АС // П₁. Предположим, что АВ не параллельна П₁ (если AB // П₁, то плоскость угла BAC параллельна П₁ и по свойству 9 ортогонального проецирования имеем:

ÐBAC =ÐB₁A₁C₁ = 90°). Поскольку ÐB₁A₁C₁ Ì П₁, ÐB₁A₁C₁ = 90° и AA₁ ^ П₁, как проецирующая линия, то плоскости S(A₁B₁,AA₁) и D(A₁C₁, AA₁) взаимно перпендикулярны. В этом случае АВ и AA₁ суть наклонная и ее ортогональная проекция на плоскости D. Так как AC Ì D и АС ^ АВ, то по теореме о трех перпендикулярах имеем АС ^ AA₁, т.е. АС // П_1.

Достаточность. Пусть ÐВАС = 90°, АС // П₁. Докажем, что Ð B₁A₁C₁ = 90°. При данных условиях имеем: AB – наклонная, А₁В₁ – ее проекция на П₁. По теореме о трех перпендикулярах имеем: (АС ^ АВ, АС // П₁) Þ АС ^ А₁В₁. Из АС // П₁ следует АС // А₁С₁. Следовательно, А₁С₁ ^ А₁В₁ и ÐB₁A₁C₁ = 90°.

Из обратимости комплексного чертежа (КЧ) следует, что если А₂В₂, А₁В₁ и С₂В₂, С₁В₁ – проекции пересекающихся прямых АВ и СВ, то при выполнении одного из двух следующих проекционных условий:

1) А₁В₁ ^ С₁В₁ и А₂В₂ // x либо С₂В₂ // x;

2) А₂В₂ ^ С₂В₂ и А₁В₁ // x либо С₁В₁ // x

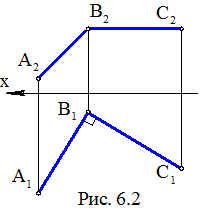в пространстве имеет место перпендикулярность АВ ^СВ (рис. 6.2).

Метрические задачи курса начертательной геометрии можно условно разделить на следующие группы:

1) построение взаимно перпендикулярных фигур:

прямых, плоскостей, прямых и плоскостей;

2) определение длин отрезков (расстояний) и

натуральной величины (НВ) плоской фигуры;

3) определение углов между фигурами.

Рассмотрим примеры решений на КЧ метрических задач в каждой группе.

Дата добавления: 2014-01-05