Теор.подобия

Она дает необходимое и достаточное условие для создания подобия. Их два:

1. Пропорциональность сходственных парам-в, входящих в условие однознач-ти

2. Равенство КП сопоставляемых явл-ий. Ф-лы размер-ти позволяют определить численные масштабные множители для пересчета соответствующих хар-к при изменении величин первич. ед. измерения. Пример: эл. схема(послед.:ист(U);R;L), П₁=L/Rt; П₂=U/Ri i=U(1-e^-Rt/L)/R;L₁/R₁t₁=L₂/R₂t₂; U₁/R₁t₁=U₂/R₂t₂ Отсюда следуют выр-я для масштабных коэф-ов: k₁=m_L/m_R m_t; k₂=m_U/m_R m_i. Масштаб независ. пр-ых можно задавать, то можно получить: m_L = k₁m_R m_t; m_U = k₂ m_R m_i. Масштаб. Коэф-ты могут быть выражены через КП.

3. Аналоговое моделирование(М-е).– изучение пр-ссов М по М имеющей др. физич. природу но подчиня-йся тем же самым мат. з-нам. Для него характерна следующая последовательность действий: 1.Необходимо определить ту физич. сис-му к-рая наиболее полно и по возможности с наименьшими затратами подходит для изучения данной физической сис-мы.

2.Необходимо получить эквивал. схему сис-мы. 3.Необходимо установить связи между сущ-ей и выбранной физич-ми схемами. Для формализации необходимо придерживаться следующих положений: 3.1.В любой схеме сущ-ют узлы(У) и элементы(Э). У устанавливают связь между выбранными Э сис-мы. Э: 2-хполюсные и многополюсные. 3.2.Состояние У опред-ся физич. перем-ой типа потенциал(Пл). 3.3.Состояние Э опис-ся фазовыми перем-ми 2-х типов: пер-я типа поток

(П) и пер-я типа разность потенциалов (РП). 4.Мат. М 2-хполюсника представляет собой компонентное ур-е (связывает либо фазовую пер-ю(относящуюся к данн. эл-ту) либо одну из этих пер-ых с некоторой величиной z (f(I,z)=0) в качестве z может быть какая либо const либо пер. типа t, либо фазовая пер-я др. эл-та. 2-х полюсники могут быть 5-ти видов:

Тип пер. Поток Раз.пот. Сопр-е Емкость Инд-ть 4.1.Пер-я типа поток I=f(z) (может означать

Электр. I U R C L источник силы, момента…)4.2.Раз. пот. U=f(z)

Пост.мех.дв. F v k m E(упру-ть) (ист. скорости)4.3. I_R=U_R/R –комплексное ур-е

Вращ.м.дв. М w k Y E(гибк-ть) для эл-та типа R. 4.4. I_С=CdU_С/dt - --//-- C

Тепл.сис. Ф(теп.пот.) Т R_T(теплопр) C_T(теплоем) -- 4.5. U_L=L dI_L/dt - --//-- L. 5.Ур-я связей между

Гидравл.с. Q(расход) P(дав.) R_Г C_Г L_Г ур-ями наз-ся топологическими. 5.1.Условие равновесия в У: åI_i =0. 5.2. В замкнутом контуре: åU_i =0 (И 1-е и 2-е ур-я для фазовых пер-ых).

4. Решение систем линейных уравнений методом Гаусса. Контроль точности

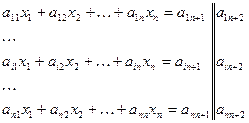
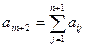
С этими элементами контрольных сумм при решении выполняются все те же действия что и с элем соотв строк, т.е. на каждом шаге выполнения должно выполняться равенство контрольных сумм. Если равенство не выполняется потеряли точность

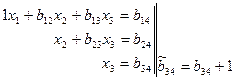
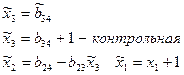
Остальные контрольные 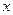вычисляются по тем же ф-ам что и обычные 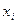только в правую часть подставляются контрольные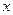

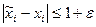
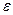– заданная точность решения

Если хотя бы 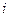-ое неравенство не выполняется, то вычисляется невязки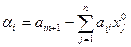 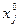– первоначальное решение системы методом Гаусса

Составляем новую систему

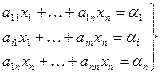
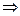
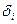
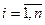- поправки

Тогда истинное решение ,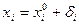

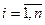
Метод Гаусса имеет ряд модификаций

1. Метод Главного элемента

2. Метод Жордано (на каждом шаге главный элемент)

3. 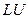– разложение

Метод простой итерации

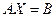Задан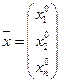

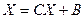(1) – итерация

Подставим нулевой вектор в правую часть

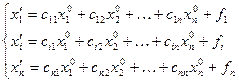
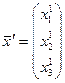
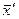подставим в правую часть системы (1) и получим

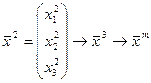– решение данной системы

Если процесс сходится

Сходится 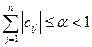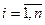Сумма всех элементов строки <1

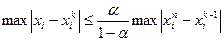
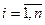
Решение 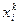отличается от истинного значения 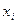не больше чем на величину в правой части при выполнении условия сх-ти

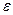–точность решения итерации будет выполняться до тех пор пока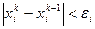

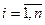
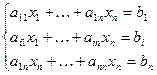
1.

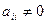
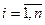
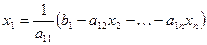
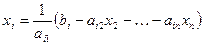
Тогда в качестве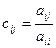

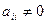
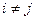
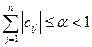
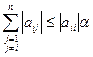– условие сх-ти для этого метода

След в исходной матрице в каждой строке модули диагонального элемента больше суммы модулей всех остальных элементов

2 способ

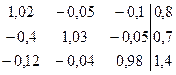
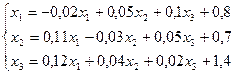
Область применения метода простой итерации очень узкая, но в случае сходимоти сх-ся довольно быстро ~n

Сложность метода 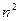Выиграли во времени. Погрешность вычисления оказывается на результате меньше чем при Гауссе. Если на каждом этапе возьмем 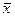, то будет рассматриваться как новое начальное условие. Если в левой части много нулей.

При решении реальных задач 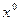выбирается из физической сути задач

3. Метод Зенделя

на 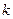-шаге получили 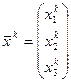на 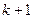шаге воспользуемся

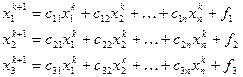
Достигается более быстрая сходимость метода

Дата добавления: 2014-01-05