Решение обыкнов. Диф. уравнений

Чтобы решить обычное дифер. Ур-е необходимо знать значение зависимой переменной и ее произв при некотрых значениях независимой переменной. Эти дополн условия задаются при 1 или нескольк зависим перемененных. Если при 1 зн-ие то такая задача наз-тся задачей начал. Условиями (Задача Коши) Если дополн условия 2, то задача наз. Краевая, а дополн. Зн-ия наз. Граничными. Решаются задачи разными способами.

Задача Каши записывается

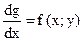
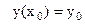Надо наити вычисляется значение произв приращения 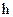по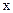Переходим к новой точке 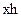положениеновой точки определяются по наклону кривой вычисленные с помощью заданного диф ур-ия Таким образом численно диф уравнения есть последовательность коротких отрезков которымиапроксимируется истиная кривая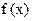

2 типа методов:

1 одношаговые методы

для нахождения следующей точки требуется инф. Лищь об. одной прдыдущей точки: метод Эллера, метод Рунге-Кутта

2метод Прогноза к корекции (многошаговые методы)

для отыскания след точки на кривой требуется информ о нескольких предыдущих точек- итерационные. Метод Мила, Адамса, Хэминга,

Обыкновенные дифференциальные уравнения (ОДУ) широко используются для математического моделирования процессов и явлений в различных областях науки и техники. Переходные процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью ОДУ.

В дифференциальное уравнение n-го порядка в качестве неизвестных величин входят функция y(x) и ее первые n производных по аргументу x

j(x, y, y¹,... y⁽ⁿ⁾ )=0. 1.1

Из теории ОДУ известно, что уравнение (1.1) эквивалентно системе n уравнений первого порядка

j_k(x, y_1, y₁^’,y₂,y₂ ^’,...,y_n,y_n ^’)=0. 1.2

где k=1,..., n.

Уравнение (1.1) и эквивалентная ему система (1.2) имеют бесконечное множество решений. Единственные решения выделяют с помощью дополнительных условий, которым должны удовлетворять искомые решения. В зависимости от вида таких условий рассматривают три типа задач, для которых доказано существование и единственность решений.

Первый тип – это задачи Коши, или задачи с начальными условиями. Для таких задач кроме исходного уравнения (1.1) в некоторой точке xo должны быть заданы начальные условия, т.е. значения функции y(x) и ее производных

y(x₀)=y₀^’, y^’(x₀)=y₁₀,..., y^(n-1)(x₀)=y_n-1,₀.

Для системы ОДУ типа (1.2) начальные условия задаются в виде

y₁(x₀)=y₁₀ , y₂(x₀)=y₂₀,..., y_n(x₀)=y_n0. 1.3

Ко второму типу задач относятся так называемые граничные, или краевые задачи, в которых дополнительные условия задаются в виде функциональных соотношений между искомыми решениями. Количество условий должно совпадать с порядком n уравнения или системы. Если решение задачи определяется в интервале x є [x₀,x_k], то такие условия могут быть заданы как на границах, так и внутри интервала. Минимальный порядок ОДУ, для которых может быть сформулирована граничная задача, равен двум.

Третий тип задач для ОДУ – это задачи на собственные значения. Такие задачи отличаются тем, что кроме искомых функций y(x) и их производных в уравнения входят дополнительно m неизвестных параметров l1,l2,¼, хm, которые называются собственными значениями. Для единственности решения на интервале [x0,xk] необходимо задать m+n граничных условий. В качестве примера можно назвать задачи определения собственных частот, коэффициентов диссипации, структуры электромагнитных полей и механических напряжений в колебательных системах, задачи нахождения фазовых коэффициентов, коэффициентов затухания, распределения напряженностей полей волновых процессов и т.д.

К численному решению ОДУ приходится обращаться, когда не удается построить аналитическое решение задачи через известные функции. Хотя для некоторых задач численные методы оказываются более эффективными даже при наличии аналитических решений.

Большинство методов решения ОДУ основано на задаче Коши, алгоритмы и программы для которой рассматриваются в дальнейшем.

Разбор и рассмотрение методов, применяемых на практике для решения дифференциальных уравнений, мы начнем с их широкой категории, известной под общим названием методов Рунге-Кутта.

Методы Рунге-Кутта обладают следующими свойствами:

1. Эти методы являются одноступенчатыми: чтобы найти у_m+1, нужна информация о предыдущей точке xm,ym.

2. Они согласуются с рядом Тейлора вплоть до членов порядка hp, где степень р различна для различных методов и называется порядковым номером или порядком метода.

3. Они не требуют вычисления производных от f (x,y), а требуют вычисления самой функции.

Рассмотрим сначала геометрическое построение и выведем некоторые формулы на основе геометрических аналогий. После этого мы подтвердим полученные результаты аналитически.

Предположим, нам известна точка xm,ym на искомой кривой. Тогда мы можем провести прямую линию с тангенсом угла наклона у¢_m=f(x_m,y_m), которая пройдет через точку x_m,y_m. Это построение показано на рис.1, где кривая представляет собой точное, но конечно неизвестное решение уравнения, а прямая линия L1 построена так, как это только что описано.

Тогда следующей точкой решения можно считать ту, где прямая L₁ пересечет ординату, проведенную через точку x=x_m+1=x_m+h.

Уравнение прямой L₁ выглядит так: y=y_m+y¢_m(x-x_m) так как y¢=f(x_m,y_m) и кроме того, x_m+1=x_m+h тогда уравнение примет вид

y_m+1=y_m+h*f(x_m,y_m) 1.1

Ошибка при x=x_m+1 показана в виде отрезка е. Очевидно, найденное таким образом приближенное значение согласуется с разложением в ряд Тейлора вплоть до членов порядка h, так что ошибка ограничения равна e_t=Кh2

Заметим, что хотя точка на графике 1 была показана на кривой, в действительности y_m является приближенным значением и не лежит точно на кривой.

Формула 1.1 описывает метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Отметим, что метод Эйлера является одним из методов Рунге-Кутта первого порядка.

Рассмотрим исправленный метод Эйлера и модификационный метод Эйлера. В исправленном методе Эйлера мы находим средний тангенс угла наклона касательной для двух точек: x_m,y_m и x_m+h,y_m+hy¢_m. Последняя точка есть та самая, которая в методе Эйлера обозначалась x_m+1,y_m+1. Геометрический процесс нахождения точки x_m+1,y_m+1 можно проследить по рис.2. С помощью метода Эйлера находится точка x_m+h,y_m+hy¢_m, лежащая на прямой L₁. В этой точке снова вычисляется тангенс, дает прямую Ĺ. Наконец, через точку x_m,y_m мы проводим прямую L, параллельную Ĺ. Точка, в которой прямая L пересечется с ординатой, восстановленной из x=x_m+1=x_m+h, и будет искомой точкой x_m+1,y_m+1.

Тангенс угла наклона прямой Ĺ и прямой L равен

Ф(x_m,y_m,h)=½[f(x_m,y_m)+f(x_m+h,y_m+y¢_mh)] 1.2

где y¢_m=f(x_m,y_m) 1.3

Уравнение линии L при этом записывается в виде

y=y_m+(x-x_m)Ф(x_m,y_m,h),

так что

y_m+1=y_m+hФ(x_m,y_m,h). 1.4

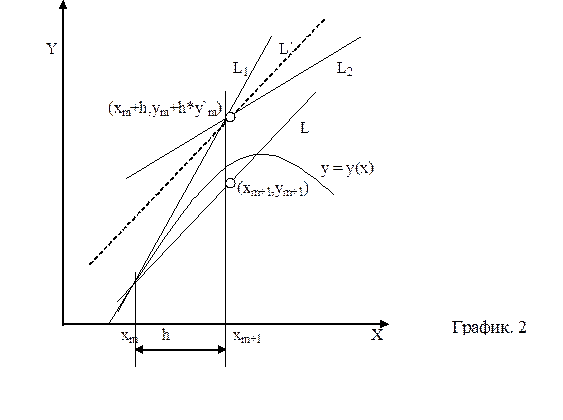
Соотношения 1.2, 1.3, 1.4 описывают исправленный метод Эйлера.

Чтобы выяснить, насколько хорошо этот метод согласуется с разложением в ряд Тейлора, вспомним, что разложение в ряд функции f(x,y) можно записать следующим образом:

f(x,y)=f(x_m,y_m)+(x-x_m)¶f/¶x+(y-y_m)¶f/¶x+¼ 1.5

где частные производные вычисляются при x=x_m и y=y_m.

Подставляя в формулу 1.5 x=x_m+h и y=y_m+hy¢_m и используя выражение 1.3 для y¢_m, получаем

f(x_m+h,y_m+hy¢_m)=f+hf_x+hff_y+O(h2),

где снова функция f и ее производные вычисляются в точке x_m,y_m. Подставляя результат в 1.2 и производя необходимые преобразования, получаем

Ф(x_m,y_m,h)=f+h/2(f_x+ff_y)+O(h2).

Подставим полученное выражение в 1.4 и сравним с рядом Тейлора

y_m+1=y_m+hf+h2/2(f_x+ff_y)+O(h3).

Как видим, исправленный метод Эйлера согласуется с разложением в ряд Тейлора вплоть до членов степени h2, являясь, таким образом, методом Рунге-Кутты второго порядка.

Рассмотрим модификационный метод Эйлера. Рассмотрим рис.3 где первоначальное построение сделано так же, как и на рис.2. Но на этот раз мы берем точку, лежащую на пересечении этой прямой и ординатой x=x+h/2. На рисунке эта точка образована через Р, а ее ордината равна y=y_m+(h/2)y¢_m. Вычислим тангенс угла наклона касательной в этой точке

Ф(x_m,y_m,h)=f+(x_m+h/2,y_m+h/2*y¢_m), 1.6

где y¢_m=f(x_m,y_m) 1.7

Прямая с таким наклоном, проходящая через Р, обозначена через L*. Вслед за тем, мы проводим через точку xm,ym прямую параллельную L*, и обозначаем ее через L₀. Пересечение этой прямой с ординатой x=x_m+h и даст искомую точку x_m+1,y_m+1. Уравнение прямой можно записать в виде y=y_m+(x-x_m)Ф(x_m,y_m,h),

где Ф задается формулой 1.6. Поэтому

y_m+1=y_m+hФ(x_m,y_m,h) 1.8

Соотношения 1.6, 1.7, 1.8 описывают так называемый модификационный метод Эйлера и является еще одним методом Рунге-Кутта второго порядка. Обобщим оба метода. Заметим, что оба метода описываются формулами вида

y_m+1=y_m+hФ(x_m,y_m,h) 1.9

и в обоих случаях Ф имеет вид

Ф(x_m,y_m,h)=a₁f(x_m,y_m)+a₂f(x_m+b₁h,y_m+b₂hy¢_m), 1.10

где y¢_m=f(x_m,y_m) 1.11

В частности, для исправленного метода Эйлера

a₁=a₂=1/2;

b₁=b₂=1.

Дата добавления: 2014-01-05