Частотные критерии устойчивости

Частотные критерии устойчивости позволяют судить об устойчивости сис­тем автоматического управления по виду их частотных характеристик. Эти кри­терии позволяют сравнительно просто исследовать устойчивость систем высокого порядка, а также имеют геометрическую интерпретацию и наглядность.

Принцип аргумента. Частотные критерии устойчивости динамических сис­тем базируются на принципе аргумента.

Пусть дан некоторый полином n-ой степени D(s)=a₀Sⁿ+a_Is^n-1+...+a_n.(10)

Этот полином представлен в виде произведения сомножителей

D(s)= a₀(s-s₁)(s-s₂)…(s-s_n) (11)

где s₁ s₂,...,s_n - корни характеристического уравнения D(s)=0.

Характеристический вектор можно тогда представить в следующем виде:

D(jω)=a₀(jω-s₁)(jω-S₂)...(jω-S_n). (12)

Каждая из скобок представляет собой комплексное число. Следовательно, D(jω) представляет собой произведение п комплексных чисел. При перемноже­нии аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектора D(jω) при изменении частоты о от нуля до бесконечности будет равен сумме углов поворота отдельных сомножителей

(12):

Ψ=ψ₁ +ψ ₂+... + ψ_п. (13)

Условимся считать вращение против часовой стрелки положительным.

Определим каждое слагаемое (13) в отдельности.

1. Пусть какой-либо корень, например s, является вещественным и отрицательным, т.е. S₁ = -α₁ где α₁ >0. Сомножитель в выражении (12), определяемый этим корнем, будет иметь вид (Jω +α₁).

Построим годограф этого вектора на комплексной плоскости при изменении частоты от нуля до бесконечности (рис,2,а). При ω=0 вещественная часть равна a_t, a мнимая нуль. Этому соответствует точка А, лежащая на оси вещественных. При увеличении частоты до бесконечности конец вектора уходит в бесконечность, причем конец вектора все время остается на вертикальной прямой.

Годографы характеристического вектора для S₁ = -a ±jβ,s₂= a±jβ.

При увеличении ω от нуля до бесконечности концы обоих векторов уходят вверх в бесконечность, и оба вектора в пределе сливаются с осью мнимых.

Результирующий угол поворота первого вектора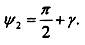

Результирующий угол поворота второго вектора

Вектор, соответствующий произведению (jω +α - jβ)(jω+α+jβ),
повернется на угол

4. Пусть те же комплексные корни имеют положительную вещественную часть, т.е. s_1,2 =+α±jβ. Проводя построения, аналогичные предыдущим (рие.3,6), можно получить, что результирующий угол поворота вектора, соответ­ствующего произведению двух сомножителей, будет

Предположим, что полином D(s) имеет 1 правых корней и (n-1) левых кор­ней.

Получаем следующую формулировку принципа аргумента: изменение (при­ращение) аргумента D(Jω) при изменении частоты со от 0 до со равно разно­сти между числом левых и правых корней уравнения D(s) =0, умноженной на π/2

Для того, чтобы линейная система была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой полуплоскости комплексного переменного s, т.е. чтобы 1=0. В этом случае согласно (14)

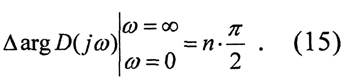
§4. Критерий устойчивости Михайлова

Рассмотрим левую часть характеристического уравнения (11), которая

представляет собой характеристический полином:

D(S) =a₀sⁿ+a₁ s^n-3 +...+a_n-1s + a_n. (l6)

Заменим в этом полиноме s = ω, где ω представляет собой угловую частоту

колебаний, соответствующих чисто мнимому корню характеристического

уравнения. При этом получим характеристический вектор

D(jω) = а₀(Jω)ⁿ + а₁(Jω)^n-1 +... + a_n-1 Jω + а_п = Re D(jω) + JmD(jω) = X(ω) + jY(ω) (17)

где вещественная часть будет содержать четные степени ω: X(ω) = ReD(jω) = a_n-a_n-₂aω²+... (18)

а мнимая - нечетные степени ω:

Y(ω) = JmD(jω) = а _{n - 1} ω – а_{n - 2}ω³ +... (19)

Из формулы (15) следует формулировка критерия устойчивости Михайлова. Система автоматического управления устойчива, если при

изменении частоты ω от 0 до ∞ вектор D(j ω) поворачивается на угол 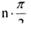степень характеристического уравнения D(s)=0.

Вектор D(jco) при изменении частоты от нуля до ∞ (0 < ω <∞) вычертит в плоскости комплексного переменного некоторую кривую (годогфаф), которая

называется кривой Михайлова.

Тогда критерий Михайлова можно сформулировать: система устойчива, если годограф D(jco) с ростом частоты от нуля до ор, начинаясь на действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) п квадрантов.

Практически годограф Михайлова строится по точкам, причем зада­ются различные значения частоты со и по формулам (18) и (19) вычисля­ются Х((й) и Y((o). Результаты расчетов сводятся в таблицу, по которой и строится годограф.

Оказывается, что годограф Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причем конец его уходит в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического полинома (рис.4).

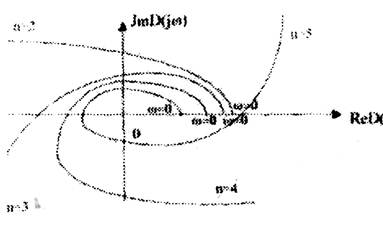
Рис.4. Частотный годограф Михайлова для устойчивых систем порядка п. Неустойчивость системы всегда связана с тем, что в годографе Михайлова нарушается последовательность прохождения квадрантов, вследствие чего

угол поворота вектора D(jω) оказывается меньшим, чем п*π/2

Рис.5. Частотный годограф Михайлова для неустойчивых систем четвертого порядка.

Наличие границы устойчивости всех трех типов рассмотрим на примере

системы четвертого порядка

В случае границы устойчивости первого типа (нулевой корень) отсутствует свободный член характеристического полинома а_п-0, т.е. а₄=0 и кривая Михайлова идет из начала координат (рис 6,а).

При границе устойчивости второго типа (колебательная граница устойчивости) характеристический полином обращается в нуль при подстановке s = jω₀

D(jω₀)=X(ω₀)+jY(ω₀)=0

откуда вытекают два равенства:

Это значит, что точкаω=ω_о на кривой Михайлова попадает в начало координат (рис.6,6). При этом величина ω_о есть частота незатухающих колебаний.

Для границы устойчивости третьего типа (бесконечный корень) конец годографа Михайлова перебрасывается, как показано на рис.6,в. При этом коэффициент а_о характеристического полинома D(s), будет проходить через нулевое значение, меняя знак плюс на минус.

Рис.6. Кривая Михайлова для границ устойчивости первого, второго и третьего типа.

Дата добавления: 2014-01-05