Определение расстояния между скрещивающимися прямыми

Приведем без доказательств сведения из стереометрии, необходимые для решения названной задачи.

1. Общим перпендикуляром двух скрещивающихся прямых называется отрезок,

концы которого лежат на данных прямых и который перпендикулярен к ним.

2. Общий перпендикуляр двух скрещивающихся прямых существует и единствен.

3. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.

Задача. Даны скрещивающиеся прямые АВ и CD. Определить расстояние между прямыми (рис. 8.7).

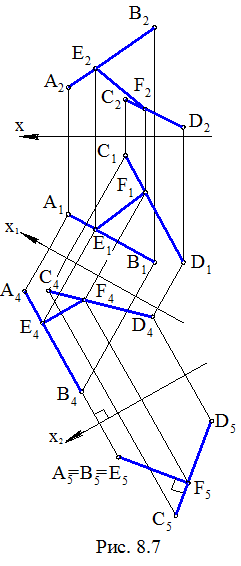Решение задачи выполним методом замены плоскостей проекций. Проекционный алгоритм решения в этом случае может быть следующим:

1) вводится новая система плоскостей проекций

П₁, П₄ , таким образом, что П₄ // АВ, т.е. на КЧ

строится ось х₁ // А₁В₁;

2) на П₄ строятся новые проекции А₄В₄ (НВ отрезка АВ) и C₄D₄ ;

3) вводится новая система плоскостей П₄, П₅ с

осью х₂ ^ А₄В₄ такая, что П₅ ^ AB;

4) на П₅ строятся новые проекции – отрезок C₅D₅ и точка А₅ = В₅;

5) строится перпендикуляр E₅F₅ ^ C₅D₅ из точки

Е₅(= А₅ = В₅);

В итоге, по смыслу построений в методе замены плоскостей проекций и приведенному понятию расстояния между скрещивающимися прямыми, получаем, что r(E₅, C₅D₅) = r(AB, CD). Для полноты решения задачи необходимо вернуть отрезок EF длиной r(AB, CD) на исходные плоскости проекций:

1) строим E₄F₄ // x₂;

2) строим E₁F₁ по проекциям E₅F₅, E₄F₄ ; E₂F₂ по проекциям E₄F₄ , E₁F₁ .

Отрезки E₂F₂ , E₁F₁ представляют собой основные проекции отрезка EF.

В стереометрии известно еще одно определение рассматриваемого расстояния: расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведенными через эти прямые.

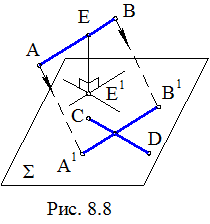Такое определение расстояния позволяет предложить более короткий путь решения рассматриваемой задачи. Пусть AB и CD – скрещивающиеся прямые (рис. 8.8). Переместим в пространстве прямую АВ параллельно самой себе в положение А¹В¹ до пересечения с CD. Если взять теперь на прямой АВ любую точку Е и опустить из этой точки перпендикуляр ЕЕ¹ на образовавшуюся плоскость Σ(CD, A¹B¹), то длина этого перпендикуляра будет искомым расстоянием r(AB,CD). Рассмотрим проекционное решение задачи.

Задача. Даны скрещивающиеся прямые АВ и CD (рис. 8.9). Определить расстояние между ними.

Решение задачи может быть следующим.

1. Перенесем прямую АВ параллельно самой себе до пересечения с CD. Таких

переносов может быть бесконечное множество. Один из переносов, например

А₁В₁ ® А₁¹В₁¹ , А₂В₂ = А₂¹В₂¹ – наиболее простой для данного КЧ вариант.

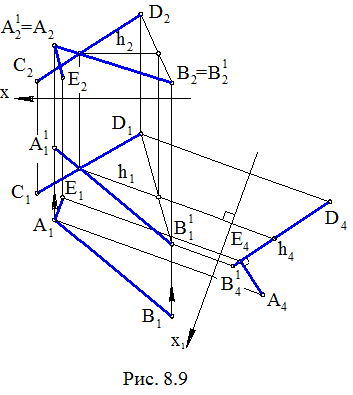2. Получаем новые условия задачи: задана плоскость Σ (А¹В¹ , CD), где А¹В¹ Ç CD и точка А; требуется определить расстояние r(А, Σ). Решение задачи выполняется методом замены плоскостей проекций по ранее изложенной схеме проекционного решения.

Дата добавления: 2014-01-05