Контур и очерк поверхности

Понятие поверхности

ПОВЕРХНОСТИ

В начертательной геометрии поверхности рассматриваются как множество последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Такой способ образования поверхности называется кинематическим.

Линия (кривая или прямая) движется в пространстве по определенному закону и создает поверхность. Она называется образующей. В процессе образования поверхности она может оставаться неизменной или менять свою форму. Закон перемещения образующей задается в виде совокупности линий и указаний о характере перемещения образующей. Эти линии называются направляющими.

Кроме кинематического способа, поверхность может быть задана

· аналитически, т. е. описана математическим выражением;

· каркасным способом, который используется при задании сложных поверхностей; каркас поверхности представляет собой упорядоченное множество точек или линий, принадлежащих поверхности.

Чтобы задать поверхность на комплексном чертеже, достаточно иметь на нем такие элементы поверхности, которые позволяют построить каждую ее точку. Совокупность этих элементов называется определителем поверхности.

Определитель поверхности состоит из двух частей:

· геометрической части, включающей постоянные геометрические элементы (точки, линии), которые участвуют в образовании поверхности;

· алгоритмической части, задающей закон движения образующей, характер изменения ее формы.

В символическом виде определитель поверхности F можно записать в виде: F(Г)[A], где Г – геометрическая часть определителя, А – алгоритмическая.

Чтобы у поверхности выделить определитель, следует исходить из кинематического способа ее образования. Но так как многие одинаковые поверхности могут быть получены различными путями, то они будут иметь различные определители. Ниже будут рассмотрены наиболее распространенные поверхности в соответствии с классификационными признаками, приятыми в курсе начертательной геометрии.

Чтобы задать поверхность на комплексном чертеже достаточно указать проекции не всего множества точек и линий, принадлежащих поверхности, а только геометрических фигур, входящих в состав ее определителя. Такой способ задания поверхности позволяет построить проекции любой ее точки. Задание поверхности проекциями ее определителя не обеспечивает наглядность, что затрудняет чтение чертежа. Для повышения наглядности, если это возможно, на чертеже указывают очерковые линии (очерки) поверхности.

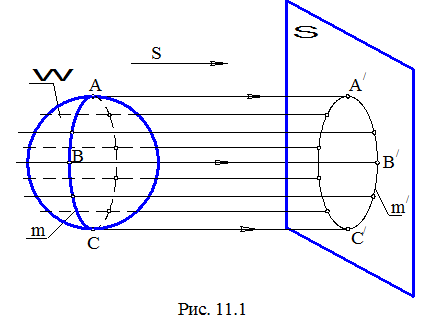
Когда какая-нибудь поверхность Wпроецируется параллельно на плоскость проекций S, то проецирующие прямые, касающиеся поверхности W, образуют цилиндрическую поверхность (рис. 11.1). Эти проецирующиеся прямые касаются поверхности Wв точках, образующих некоторую линию m,котораяназывается контурной линией.

Проекция контурной линии m на плоскость S – m^/,называется очерком поверхности. Очерк поверхности отделяет проекцию поверхности от остальной части плоскости проекций.

Контурную линию поверхности используют при определении видимости точек относительно плоскости проекций. Так, на рис. 11.1 проекции точек поверхности W, расположенные левее контура m, на плоскости S будут видимыми. Проекции остальных точек поверхности будут невидимыми.

Дата добавления: 2014-01-05