Второй аспект

Основной вопрос в определении безрискового эквивалента состоит в установлении баланса между денежным потоком, подверженным риску, и эквивалентной безрисковой суммой. Чем меньше будет отличаться величина безрискового эквивалента от исходной суммы, тем большим будет принятие риска у инвестора и наоборот. В терминах теории полезности такая задача – отношение инвестора к риску – решается с помощью построения кривых безразличия. См. рисунок.

Можно дать следующую интерпретацию графика. Рассматриваются два проекта А и Б, ожидаемые доходы которых составляют 150 и 300 при уровне риска, соответственно, β_А и β_Б. При таком положении дел для инвестора оба проекта являются равнозначными. То есть, проект А, дающий доход 150 и уровень риска которого - β_А, эквивалентен более рисковому проекту Б, но обладающим большим значением дохода. Вместе с тем, существует еще одна возможность – реализовать проект В: при нулевом уровне риска получить доход в размере 100. С точки зрения инвестора, такой проект равновозможен наряду с предыдущими двумя. И поскольку этот последний является безрисковым, то доходы по нему могут считаться безрисковым эквивалентом каждому из рассмотренных денежных потоков по проектам А и Б соответственно.

Рассмотрим определение безрискового эквивалента с позиций функции полезности.

Пример. Объем инвестиций в проект составляет 20000, а ежегодные поступления по нему предполагаются из расчета 4000 с вероятностью 30% или 7000 с вероятностью 70%. Требуется оценить эффективность проекта, учитывая, что ставка дисконтирования равна 10,5% годовых, а срок реализации – 6 лет.

Решение. Ежегодный средний ожидаемый доход по проекту составляет

С_N = 4000 * 0,3 + 7000 * 0,7 = 6100.

Отсюда можно определить значение чистой приведенной стоимости проекта:

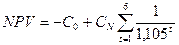=-20000+6100*4б29 = 6182.

Поскольку полученное значение ожидаемых платежей является величиной рисковой, то может быть определен ее безрисковый эквивалент.

Можно предположить, что для данного проекта имеется функция полезности U(c), изображенная на рис.

В таком случае полезность дохода в 4000 составляет U_A, а полезность дохода в 7000 – U_В.

U_N = U(C_N) = U(4000*0,3+7000*0,7) = 0,3 * U(4000) + 0,7 * U(7000).

Получим, что U_N < U(6100), т.е. полезность дохода в 6100 оказывается меньше рисковых ожиданий инвестора. С точки зрения инвестора действительная полезность дохода в 6100 равна значению полезности с абсциссой C_М = 4800, т.е. равна величине U_М = U_N = U(C_М) = U(4800).

Тогда с учетом, с учетом предпочтений инвестора – его отношения к риску – безрисковым эквивалентом рисковой суммы следует считать величину C_М = 4800 и, исходя из этого значения, рассчитать NPV проекта:

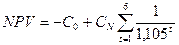= -20000 + 4800 * 4,29 = 602.

То есть проект оказывается окупаемым. Плата за риск составила 6182 – 602 = 5580.

Дата добавления: 2014-01-05