Рыночный портфель

Другим важным свойством САРМ является то, что в состоянии равновесия каждый вид ценных бумаг имеет ненулевую долю в «касательном» портфеле. Это означает, что в состоянии равновесия доля любой ценной бумаги в портфеле p отлична от 0. Основанием этого свойства является теорема разделения, которая утверждает, что доля рискованных ак­тивов в портфеле каждого инвестора не зависит от предпочтения инвестора относи­тельно риска и доходности. Эта теорема основывается на том, что рискованная доля портфеля каждого инвестора представляет собой просто инвестирование в p. Если каж­дый инвестор приобретает p при этом p не включает в себя инвестиции в каждый вид бумаг, то получается, что никто не инвестировал в те бумаги, которые имели нулевую долю в p. Это должно привести к тому, что курсы ценных бумаг с нулевой долей упадут, вызвав рост их ожидаемой доходности до тех пор, пока в «касательном» портфели их доля станет отличной от 0.

Может возникнуть и другая интересная ситуация. Что произойдет, если каждый инвестор придет к выводу, что доля акций Х в «касательном» портфеле должна составлять 0,40, но по текущему курсу спрос на эти акции превышает предложение? В этом случае поток поручений на покупку будет слишком велик и брокеры будут вы­нуждены поднимать цену. Это приведет к снижению ожидаемой доходности этих акций, сделает их менее привлекательными и тем самым уменьшит их долю в «касатель­ном» портфеле до величины, при которой спрос на них будет равен предложению.

В итоге все будет сбалансировано. Когда прекратятся все изменения курсов, рынок займет положение равновесия. При этом, во-первых, каждый инвестор захочет держать определенное положительное число рискованных бумаг каждого вида. Во-вторых, те­кущий рыночный курс каждой ценной бумаги будет находиться на уровне, уравнове­шивающем спрос и предложение. В-третьих, величина безрисковой ставки будет та­кой, что общая сумма денежных средств, взятых в долг, будет равна обшей сумме денег, предоставленных взаймы. В результате соотношение долей каждой бумаги в «касатель­ном» портфеле в состоянии равновесия будет соответствовать соотношению долей бумаг в так называемом рыночном портфеле (market portfolio), которому дано следующее определение:

Рыночный портфель – это портфель, состоящий из всех ценных бумаг, в котором доля каждой соответствует ее относительной рыночной стоимости.

Причина, по которой рыночный портфель занимает центральное место в САРМ, заключается в том, что эффективное множество состоит из инвестиций в рыночный портфель в совокупности с желаемым количеством безрискового заимствования или кредитования.

Итак, регрессионная модель для i – й ценной бумаги имеет следующий вид

,

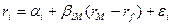где β_iM – показатель, характеризующий взаимосвязь доходности ценной бумаги и доходности рыночного (касательного) портфеля.

Имеет место следующая теорема.

Теорема. Для всех ценных бумаг, обращающихся на рынке, коэффициент α_i один и тот же и равен безрисковой ставке.

Имеем

.

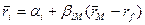Рассмотрим портфель p, состоящий из i – й ценной бумаги и рыночного портфеля М в пропорции x_i и 1 - x_i соответственно. Ожидаемая доходность такого портфеля составит

,

а стандартное отклонение будет

,

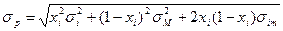где σ_im – ковариация актива i с рыночным портфелем.

Все такие портфели отображаются на кривую, соединяющую точки i и М.

Дата добавления: 2014-01-05