Развертки гранных поверхностей

Развертки поверхностей

Определение. Если поверхность, представляемую в виде тонкой, гибкой и нерастяжимой пленки, можно путем изгибания совместить с плоскостью без разрывов и складок, то поверхность, обладающая этим свойством, называется развертывающейся, а фигура, полученная в результате совмещения поверхности с плоскостью, называется разверткой. В математике доказано, что к развертывающимся относятся лишь три группы линейчатых поверхностей: конические, цилиндрические и торсовые (поверхности касательных к пространственной кривой). У этих поверхностей вдоль каждой прямолинейной образующей существует единственная касательная плоскость, у остальных линейчатых поверхностей вдоль образующей прямой существует бесконечное множество таких плоскостей. Изгибание поверхности на плоскость приводит к соответствию, устанавливаемому между множеством точек поверхности и множеством точек ее развертки. Это соответствие обладает следующими свойствами:

1) точке поверхности соответствует единственная точка развертки и наоборот;

2) длины соответственных линий поверхности и ее развертки равны;

3) углы, образованные линиями на поверхности, равны углам, образованным соответствующими линиями на развертке;

4) площади соответственных фигур на поверхности и на развертке равны.

Из приведенных свойств вытекают следствия:

1) прямая линия поверхности преобразуется в прямую линию развертки;

2) параллельные линии поверхности преобразуются в параллельные прямые ее

развертки.

Для развертывающихся линейчатых поверхностей строятся графически приближенные развертки, поскольку в процессе построения развертки эти поверхности заменяются (аппроксимируются) вписанными или описанными многогранными поверхностями. Точные развертки аппроксимирующих многогранных поверхностей принимаются за приближенные развертки развертывающихся поверхностей. Для поверхностей, которые не являются развертывающимися, строятся условные развертки по следующей схеме:

НП Þ РП Þ ГП ~ ТР, где НП – неразвертывающая поверхность, РП – развертывающаяся поверхность, ГП – гранная поверхность, ТР – точная развертка, Þ – этап аппроксимации предыдущей поверхности последующей. Поскольку в результате последовательных аппроксимаций исходная поверхность заменяется гранной, то рассмотрим вначале построения точных разверток гранных поверхностей.

Определение. Разверткой гранной поверхности называется множество соединенных в плоскости многоугольников, конгруэнтных (равных) соответственно ее граням. Под соединением понимается последовательное размещение многоугольников развертки, которое соответствует последовательному расположению граней поверхности.

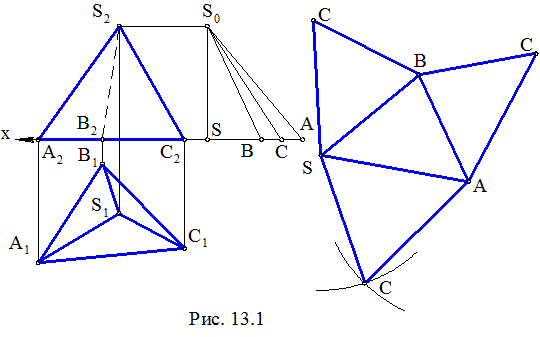
Задача. Дана пирамида SABC (рис. 13.1). Построить развертку ее поверхности.

Основание ABC пирамиды принадлежит плоскости проекций П₁, поэтому ∆A₁B₁C₁ – его НВ. Для определения НВ боковых ребер пирамиды воспользуемся методом прямоугольного треугольника (см. п. 8.1). SS₀ ^ х – общая разность высот концов ребер данной пирамиды. Откладывая от точки S по оси Х отрезки

SB = S₁B₁, SC = S₁C₁, SA = S₁A₁, получаем S₀В, S₀С, S₀А – НВ ребер пирамиды. Затем в стороне, используя известные правила построения треугольника по его сторонам, выполняем собственно построения развертки пирамиды.

Задача. Дана трехгранная призма ABCDFE (рис. 13.2). Построить развертку ее боковой поверхности.

Основания ABC и DFE данной призмы параллельны плоскости проекций П₁ и, следовательно, проецируются на эту плоскость в НВ. Каждую из боковых граней призмы представляем в виде двух треугольников, разделив грань диагональю. По методу прямоугольного треугольника определяем НВ трех диагоналей BD, BE и CD и одного ребра (ребра по условию задачи равны). В итоге на диаграмме натуральных величин отрезков получаем:

MN – общая разность высот ребер; N1 = A₁D₁ = B₁F₁ = C₁E₁; N2 = D₁C₁, N3 = B₁D₁, N4 = B₁E₁; M1 – НВ ребра, М2 – НВ диагонали DC, М3 – НВ диагонали BD и М4 – НВ диагонали ВЕ. Имея НВ ребер призмы, трех ее диагоналей и сторон треугольников оснований, строим развертку боковой поверхности как совокупности треугольников, выстраиваемых по их сторонам.

Метод, которым были построены развертки в рассмотренных двух задачах, называется методом треугольников (метод триангуляции). Метод основан на возможности построения единственного (по форме) треугольника по его заданным сторонам. Заметим, что четыре, пять, …. отрезков определяют бесконечное множество четырех, пяти, …. угольников. Метод треугольников наиболее прост и универсален при построении точных разверток гранных поверхностей, а также приближенных и условных разверток линейчатых поверхностей.

Рассмотрим специальные методы построения разверток гранных поверхностей.

Задача. Дана трехгранная призма АВСА¹В¹С¹ (рис. 13.3). Построить развертку призмы.

Для построения развертки применим метод нормального сечения. Метод применим для призматических поверхностей, у которых боковые ребра представляют собой линии уровня. Последовательность построений в методе нормального сечения следующая:

1) призма рассекается плоскостью ∆ перпендикулярно ее ребрам;

2) определяются НВ сторон многоугольника, по которым плоскость ∆ пересекает поверхность призмы;

3) многоугольник как ломаная линия разворачивается в отрезок прямой, внутри которой отмечаются точки, соответствующие вершинам многоугольника;

4) через эти точки проводятся прямые, перпендикулярные отрезку – развертке многоугольника;

5) на перпендикулярных прямых от указанных точек откладываются отрезки, представляющие НВ соответствующих отрезков ребер пирамиды;

6) концы отрезков ребер последовательно соединяются отрезками прямых линий;

7) к построенной развертке боковой поверхности достраиваются НВ многоугольников – оснований призмы.

Применим изложенную последовательность к нашей задаче. Поскольку ребра призмы АА¹, ВВ¹, СС¹ по условию задачи являются горизонталями, то А¹А¹₁, В¹В¹₁, С¹С¹₁ есть НВ этих ребер. Рассечем боковую поверхность призмы плоскостью ∆, перпендикулярной ее ребрам. Поскольку ребра являются горизонталями, то ∆ ^ П₁ и Δ₁ – горизонтальный след плоскости Δ. 1₁2₁3₁ и 1₂2₂3₂ – проекции нормального сечения призмы. Проекция Δ 1₄2₄3₄ представляет собой НВ нормального сечения, построенную методом замены плоскостей проекций, где х₁ // Δ₁. В стороне от КЧ, на горизонтальной прямой, последовательно располагаем отрезки 13 = 1₄3₄, 32 = 3₄2₄, 21 = 2₄1₄ и проводим через их концы вертикальные прямые. На этих прямых откладываем отрезки:

1В = 1₁В₁, 1В¹ = 1₁В₁¹; 3С = 3₁С₁, 3С¹ = 3₁С₁¹; 2А = 2₁А₁, 2А¹ = 2₁А₁¹.

Многоугольник ВСАВВ¹А¹С¹В¹ представляет собой развертку боковой поверхности заданной призмы. Достроив к ней ΔАВС и ΔА¹С¹В¹ , получаем полную развертку призмы.

Задача. Дана призма АВСА¹С¹В¹ (рис. 13.4). Построить ее развертку.

Для построения развертки призмы можно использовать известный метод раскатки. Его применение возможно для таких призматических поверхностей, у которых боковые ребра и плоскости оснований являются прямыми и плоскостями уровня. Суть метода заключается в последовательном вращении граней призмы вокруг ее боковых ребер до положения совмещения с плоскостью, которая проходит через одно из ребер и параллельна плоскости проекций, т.е. каждая грань оставляет свой «отпечаток» в этой плоскости. Множество последовательно полученных и расположенных «отпечатков» в плоскости представляет собой развертку боковой поверхности призмы. Рассмотрим решение данной задачи. Боковые ребра призмы являются фронталями, а плоскости оснований – горизонтальными плоскостями уровня.

Условия задачи соответствуют методу раскатки. Пусть первое вращение – вращение грани АСС¹А¹, происходит вокруг оси СС¹. Повернем эту грань до совмещения с плоскостью развертки, проходящей через ребро СС¹ и параллельной плоскости проекций П₂. В этом случае вершины А и А¹ будут вращаться в проецирующих плоскостях Ф ^ П₂ и Ф¹ ^ П₂ соответственно, которые перпендикулярны ребру АА¹. Совмещенные положения A⁰ и A⁰¹ вершин А и А¹ будут принадлежать фронтальным следам Ф₂ и Ф₂¹ плоскостей Ф и Ф¹ соответственно и отстоять от точек С₂ и С₂¹ на расстоянии С₂A⁰ = C₂¹A⁰¹ = А₁С₁ = А₁¹С₁¹ . Следующим вращением вокруг оси A⁰A⁰¹ добиваемся совмещения грани АВВ¹А¹ с плоскостью развертки. При этом совмещенные положения B⁰ и B⁰¹ вершин В и В¹ соответственно будут принадлежать фронтальным следам Δ₂ и Δ₂¹ плоскостей Δ ^ П₂ и Δ¹ ^ П₂ и отстоять от точек A⁰ и A⁰¹ на расстоянии B⁰A⁰ = B⁰¹A⁰¹ = В₁А₁ = В₁¹А₁¹. Последнее, третье вращение, будет происходить вокруг оси B⁰B⁰¹ и позволит получить совмещение грани ВСС¹В¹ с плоскостью развертки, при этом совмещенные положения C⁰ и C⁰¹ вершин С и С¹ будут принадлежать фронтальным следам Σ₂ и Σ₂¹ проецирующих плоскостей Σ ^ П₂ и Σ¹ ^ П₂ и отстоять от точек B⁰ и B⁰¹ на расстоянии C⁰B⁰ = C⁰¹B⁰¹ = С₁В₁ = С₁¹В₁¹. Полученный в итоге построений многоугольник С₂A⁰B⁰C⁰C⁰¹B⁰¹A⁰¹С₂¹ будет представлять собой развертку боковой поверхности заданной призмы.

Дата добавления: 2014-01-05