Ортогональная (прямоугольная) изометрическая проекция

Ортогональная изометрическая проекция (изометрия) является ортогональной аксонометрической проекцией при u = v = w. По формуле (14.1) получим u = =v = w = 0,82. По формуле (14.2) определим, что угол между любыми осями 120°.

Построение изометрии точки выполняется так же, как показано на рис. 14.2, 14.3. Каждую координату точки необходимо умножить на 0,82. Такая изометрия называется точной или теоретической. Если изометрию точки выполнить в масштабе 1,22: 1, то координату точки нужно умножить на 0,82 (коэффициент искажения по оси), а затем умножить на 1,22 (увеличение из-за выполнения в масштабе), и тогда изометрическая координата, например, x_A' равна 0,82×1,22×x_A = x_A. Значит, при выполнении изометрии в масштабе 1,22: 1 (масштаб приведения) можно координаты точки не умножать на коэффициенты искажения, а брать их такими же, как на комплексном чертеже. Изометрия, выполненная в масштабе 1,22: 1, называется приведенной или практической, коэффициенты искажения при этом u = v = w = 1.

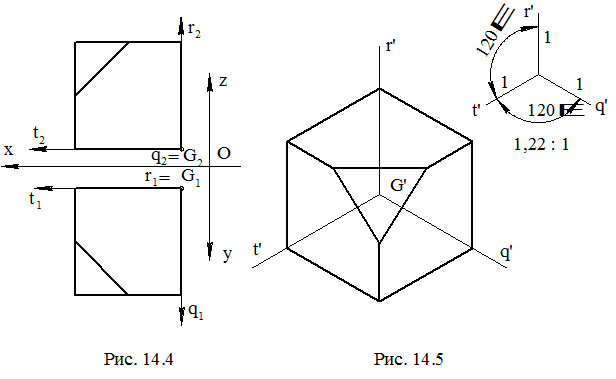На рис. 14.4 показан комплексный чертеж куба со срезанной вершиной. На рис. 14.5 построена его приведенная изометрия. Рядом с изометрией дана схема расположения изометрических осей с указанием коэффициентов искажения и масштаба приведения. На рис. 14.4 в качестве системы координат, связанной с кубом, взята Gtqr, а не система координат Oxyz комплексного чертежа, как на рис. 14.2, 14.3. Система Gtqr задана своими проекциями G₁t₁q₁r₁ и G₂t₂q₂r₂. Теперь эта система проецируется в изометрическую систему координат, и относительно нее берутся координаты вершин куба. Изометрию куба легко построить, если построить изометрию его вершин и соединить их. Постройте, в качестве упражнения, изометрию куба, связав с ним систему координат комплексного чертежа Oxyz, которая в этом случае будет проецироваться в изометрическую систему координат.

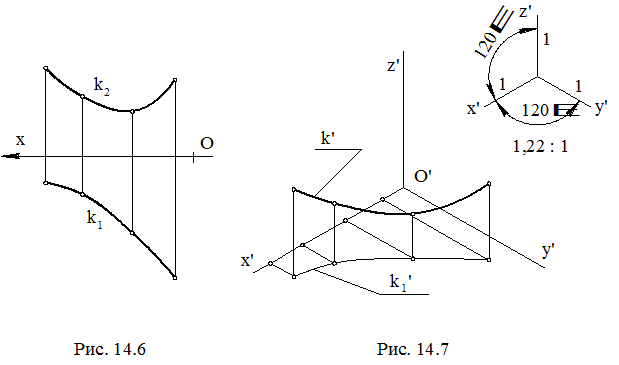На рис. 14.6 показан комплексный чертеж кривой k. На рис. 14.7 построена приведенная изометрия этой кривой. В качестве системы координат, связанной с кривой, взята система координат комплексного чертежа Oxyz, которая проецируется в изометрическую систему координат O'x'y'z'. Для построения изометрии кривой необходимо построить изометрию ряда ее точек и соединить их кривой линией. Так можно построить изометрию любой кривой, но для построения изометрии окружности удобно использовать специальные методы.

Пусть окружность диаметром d расположена в плоскости Oxy (или в плоскости, параллельной Oxy). Эта окружность проецируется на аксонометрическую плоскость в эллипс. Все диаметры эллипса, кроме одного, будут меньше диаметра окружности. Большой диаметр эллипса равен диаметру окружности и является проекцией диаметра окружности, расположенного на линии уровня, параллельной аксонометрической плоскости П'. Большой диаметр расположен на проекции линии уровня. Линия уровня «сохранит» не только длину диаметра d окружности, но и прямой угол с прямой линией, которая ей перпендикулярна (теорема о проецировании прямого угла). Ось z перпендикулярна плоскости Oxy, а значит, перпендикулярна любой прямой этой плоскости, в том числе и линии уровня. Тогда аксонометрическая проекция линии уровня, на которой расположен большой диаметр эллипса, перпендикулярна проекции оси z – аксонометрической оси z'. Малый диаметр эллипса перпендикулярен большому диаметру.

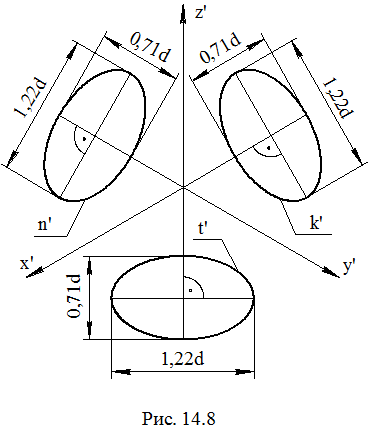При выполнении изометрии в масштабе 1,22: 1 большой диаметр будет равен 1,22d. Малый диаметр равен 0,71d (принимаем без вывода). Эллипс строится по большому и малому диаметрам. Повторяя все сказанное выше, для плоскостей Oxz и Oyz, получим расположение эллипсов, показанное на рис. 14.8. Окружность t, расположенная в плоскости Oxy или ей параллельной плоскости, проецируется на П' в эллипс t', который является изометрией окружности t. Изометрией окружности n, принадлежащей плоскости Oxz или ей параллельной плоскости, будет эллипс n'. Изометрией окружности k, принадлежащей плоскости Oyz или ей параллельной плоскости, будет эллипс k'. Изометрии окружностей, принадлежащих плоскостям Oxy, Oxz, Oyz или им параллельным плоскостям, строятся в такой последовательности: строится изометрия центра окружности; строятся большой и малый диаметры; по большому и малому диметрам строится ряд точек эллипса; точки эллипса соединяются плавной кривой.

Если окружность принадлежит плоскости общего положения, то прямой, перпендикулярной этой плоскости, на изометрии нет. Поэтому необходимо на комплексном чертеже через центр окружности провести отрезок прямой перпендикулярной плоскости окружности. Затем построить изометрию этого отрезка и провести большой диаметр перпендикулярно изометрии этого отрезка, через изометрию центра окружности. Большой диаметр равен 1,22d, где d – диаметр окружности. Далее, на комплексном чертеже окружности взять любую точку окружности и построить ее изометрию. Теперь на изометрии есть большой диаметр эллипса и одна его точка. Значит, можно выполнить построение эллипса по большому диаметру и точке.

Дата добавления: 2014-01-05