Расстояния. Псевдорешения. Нормальные решения. Нормальные псевдорешения

Расстоянием между множествами X и Y называется .

Рассмотрим задачу нахождения расстояния от точки x до подпространства W. В начале рассмотрим случай, когда подпространство задано в виде линейной оболочки системы векторов.

Теорема 2.5. Расстояние от точки до подпространства достигается на перпендикуляре, опущенном из точки x на подпространство.

Доказательство. Представим 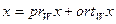. Расстояние от точки x до подпространства W равно . Векторы и ортогональны друг другу, и по неравенству Бесселя , причем равенство достигается только в случае . Тем самым установлено 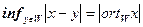, что и требовалось.

Пусть 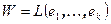и система векторов 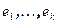линейно независимая. Расстояние от точки x до подпространства W можно найти как отношение объема k +1-мерного параллелепипеда натянутого на векторы к объему k -мерного параллелепипеда натянутого на векторы 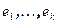. Таким образом, справедлива формула 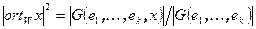. К сожалению, эта формула не позволяет находить проекцию и ортогональную составляющую вектора. Для нахождения проекции можно поступать следующим образом. 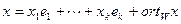Представим и , а затем умножим скалярно на векторы 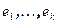вектор x. Получим систему линейных уравнений . Коэффициенты при неизвестных образуют матрицу Грама, определитель которой не равен нулю. Следовательно, система имеет единственное решение. Решив эту систему, найдем проекцию вектора x, а затем и ортогональную составляющую.

Рассмотрим случай, когда линейное подпространство задано системой однородных линейных уравнений Ax =0. Для простоты проведения рассуждений будем считать, что строки матрицы A линейно независимы. В ортонормированном базисе, коэффициенты при неизвестных в уравнении являются координатами вектора из ортогонального дополнения (см. п.2.4). Таким образом, по системе линейных уравнений можно найти базис ортогонального дополнения к пространству W. Обозначим базис через 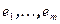. Тогда представим 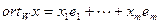и , а затем умножим скалярно на векторы 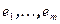вектор x. Получим систему линейных уравнений 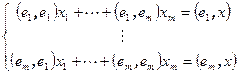. Коэффициенты при неизвестных образуют матрицу Грама, определитель которой не равен нулю. Следовательно, система имеет единственное решение. Решив эту систему, найдем ортогональную составляющую вектора x, а затем и проекцию.

Рассмотрим теперь задачу нахождения расстояния от точки x до линейного многообразия M. Эта задача легко сводится к аналогичной задаче построения расстояния от точки до подпространства. Действительно, пусть M=z + W, где z – произвольная точка из M, а W – подпространство. Тогда 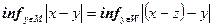, то есть задача свелась к определению расстояния от точки x-z до подпространства W.

Линейное многообразие, заданное как множество решений одного линейного уравнения ax = b называется гиперплоскостью. Рассмотрим задачу отыскания расстояния от точки y до гиперплоскости ax = b. Перпендикуляр, опущенный из y на гиперплоскость равен и . Отсюда находим неизвестный параметр , а затем и расстояние .

Рассмотрим задачу определения расстояния между двумя линейными многообразиям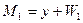и и . Расстояние между ними равно , то есть задача свелась к нахождению расстояния от точки y-z до подпространства . Заметим, что расстояние между линейными многообразиями достигается на общем перпендикуляре.

Дата добавления: 2014-01-05