Параметрические уравнения

Здесь мы поговорим о параметрических уравнениях вообще. Рассмотрим уравне­ния следующего вида:

Здесь x (t), y (t) и z (t) представляют собою функции, определённые на одном и том же про­межутке Δ = ‹α; β› и непрерывные на нём (с обычной оговоркой относительно концов). Возьмём какое-либо конкретное значение параметра t ₁ Î Δ и отметим точку с координа­тами (x (t ₁); y (t ₁); z (t ₁)). Взяв другое значение параметра, мы с помощью той же процедуры можем отметить другую точку (случайным образом она может совпасть с первой). Проде­лывая это с каждой точкой промежутка Δ (т. е. с каждым возможным значением пара­метра t), мы получим некоторую совокупность точек пространства (вообще говоря, беско­нечную), которую можно назвать линией или кривой. В такой ситуации говорят, что урав­нения (6) определяют эту кривую или являются параметрическими уравнениями этой ли­нии.

Классический пример (правда, на плоскости, а не в пространстве): уравнения

представляют собою параметрические уравнения единичной окружности.

Для аналитической геометрии важен, конечно, случай, когда параметризующие функции x (t), y (t) и z (t) линейны. Итак, рассмотрим параметрические уравнения следую­щего вида:

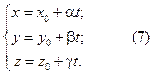
Всегда будем считать, что Δ = (−∞; ∞) = R.

Теорема. Параметрические уравнения (7) при условии l = {α; β; γ} ≠ 0 определяют в трёхмерном пространстве прямую линию, проходящую через точку M ₀ = (x ₀; y ₀; z ₀), для которой вектор l является направляющим.

Доказательство. Здесь также будем предполагать, что все три числа α, β и γ не равны нулю. Обозначим через Γ множество точек, определяемое уравнениями (7), и рас­смотрим уравнения

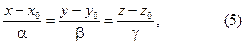
определяющие, как мы видели, прямую L, проходящую через точку M ₀ = (x ₀; y ₀; z ₀), для которой вектор l является направляющим. Нам достаточно, стало быть, доказать, что Γ = = L.

Для доказательства этого факта возьмём произвольную точку M ₁ = (x ₁; y ₁; z ₁) Î L и заметим, что для неё удовлетворяются уравнения (5):

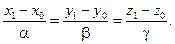
Общее значение этих трёх величин обозначим t ₁; имеем:

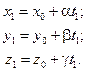
Но это означает, что M ₁ = (x ₁; y ₁; z ₁) Î Γ. Обратно, пусть точка M ₂ = (x ₂; y ₂; z ₂) Î Γ. Это означает существование такого t ₂, для которого выполняются соотношения:

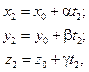
из которых немедленно получаем:

что означает, что M ₂ = (x ₂; y ₂; z ₂) Î L, QED.

[1] Я почерпнул его в учебнике П. С. Моденова «Аналитическая геометрия».

[2] От латинского слова mediocritas ‛середина’.

[3] Quod erat demonstrandum (лат.) ‛что и требовалось доказать’.

[4] Длину вектора a обозначаю | a | (аналогично для отрезка).

[5] Точнее, несущие прямые каких-нибудь (а значит, и любых) их представителей коллинеарны. Подобные замечания я уже не буду делать впредь.

[6] В математике используются три синонима: перпендикулярный, ортогональный и нормальный.

[7] От слова замостить (плоскость), однокоренного к слову мост.

[8] Carl Gustav Jacob Jacobi(Карл Густав Якоб Яко́би, 10.12.1804, Потсдам − 18.02.1851, Берлин) − из­вестный немецкий математик, родной брат российского академика, физика Бориса Семёновича Якоби.

[9] Carl Gustav Jacob Jacobi(Карл Густав Якоб Яко́би, 10.12.1804, Потсдам − 18.02.1851, Берлин) − из­вестный немецкий математик, родной брат российского академика, физика Бориса Семёновича Якоби.

Дата добавления: 2014-01-05