Способ раскатки

Способ раскатки применяется для построения разверток призматических и цилиндрических поверхностей в случае, когда боковые ребра призмы или образующие цилиндра параллельны какой-либо плоскости проекций, следовательно, проецируются в натуральную величину, а стороны основания параллельны другой плоскости проекций.

Схема построения развертки:

1. Мысленно разрезается боковая поверхность по одному из ребер.

2. Последовательным вращением вокруг боковых ребер, как вокруг линий уровня, все боковые грани совмещаются с плоскостью уровня, проходящей через ребро, по которому разрезается данная призма.

Пример 5. Построить полную развертку поверхности наклонной треугольной призмы.

Решение: Развертку боковой поверхности призмы строим способом раскатки, так как боковые ребра ее параллельны фронтальной плоскости проекций, а стороны основания параллельны горизонтальной плоскости проекций и проецируются в натуральную величину (рис. 12.6)

Так как боковые ребра параллельны фронтальной плоскости П₂, можно каждую грань повернуть вокруг соответствующего ребра до положения, когда эта грань окажется параллельна плоскости П₂. Тогда она и спроецируется на плоскость П₂ без искажения. Повернув таким образом каждую грань, получим развертку боковой поверхности призмы.

Примем за плоскость развертки плоскость Σ (Σ₁), проходящую через ребро АА', и параллельную фронтальной плоскости проекций. Совместим грань АА'В'В с плоскостью Σ. Для этого мысленно разрежем поверхность призмы по ребру АА' и повернем грань АА'В'В вокруг ребра (как вокруг фронтали) до совмещения с фронтальной плоскостью Σ, проходящей через это ребро.

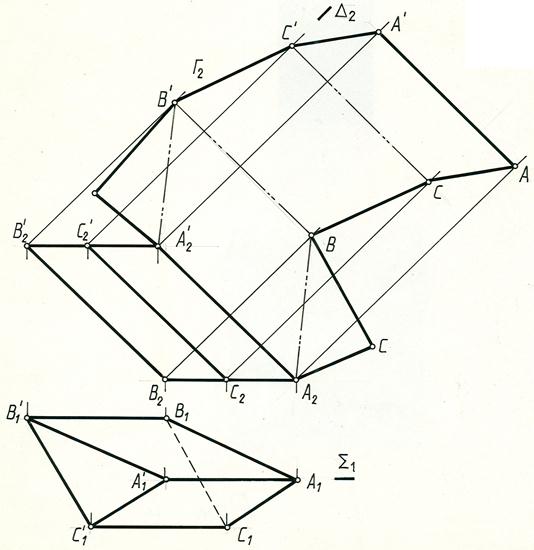
Рис. 12.6

Для определения совмещенного положения ребра ВВ' с плоскостью Σ, из точки В₂' проводим вырожденную проекцию плоскости Г(Г₂), в которой вращается точка В', (см. метод вращения вокруг линии уровня) перпендикулярную АА', на которой из точки А'₂ делаем засечку дугой окружности радиуса A₂'B'=A₁B₁. Через точку В' проводим прямую В'В параллельную А'А. Принимаем совмещенное положение ребра В'В за новую ось и вращаем вокруг нее грань В'ВСС' до совмещения с плоскостью Σ. Для этого из точки C₂' проводим вырожденную проекцию плоскости Δ (Δ₂) перпендикулярную ребру ВВ', а из точки В' – дугу окружности радиусом равным B₁C₁. Пересечение дуги с Δ ₂ определит положение точки С'. Аналогично определяем положение ребра А'А. Соединив соответствующие точки прямыми линиями, получим развертку боковой поверхности призмы. Достроив основание призмы, получим полную развертку.

Дата добавления: 2014-01-05