
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчёт сжатых элементов
|
|
|
|
Сжатые элементы бывают условно центрально сжатыми и внецентренно сжатыми.
Чистого центрального сжатия не существует по причине отклонения реальных размеров элемента от проектных, из-за неоднородности бетона и др. Поэтому при, казалось бы, центральном приложении сжимающей силы к элементу на самом деле происходит его внецентренное сжатие с так называемым. случайным эксцентриситетом  . Принято считать, что если
. Принято считать, что если 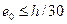 , то такой элемент допускается рассматривать как центрально сжатый (поэтому его и называют условно центрально сжатым). Правда, это может быть отнесено только к элементам прямоугольного сечения, симметрично армированным сталью классов А240, 300, 400, 500 и имеющим расчётную длину
, то такой элемент допускается рассматривать как центрально сжатый (поэтому его и называют условно центрально сжатым). Правда, это может быть отнесено только к элементам прямоугольного сечения, симметрично армированным сталью классов А240, 300, 400, 500 и имеющим расчётную длину 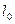
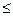 20 h.
20 h.
Расчёт условно центрально сжатых элементов по прочности производится из условий
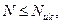 (6.26)
(6.26)
и  (47*)
(47*)
где 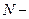 продольное сжимающее усилие от постоянных и временных (длительных и кратковременных) нагрузок (кратковременное действие);
продольное сжимающее усилие от постоянных и временных (длительных и кратковременных) нагрузок (кратковременное действие);
 продольное сжимающее усилие от постоянных и временных длительных нагрузок (длительное действие);
продольное сжимающее усилие от постоянных и временных длительных нагрузок (длительное действие);
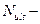 предельное значение продольной силы, которое может воспринять элемент и определяемое по формуле
предельное значение продольной силы, которое может воспринять элемент и определяемое по формуле
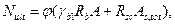 (6.27)
(6.27)
здесь 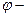 коэффициент, принимаемый при длительном действии нагрузки по таблице
коэффициент, принимаемый при длительном действии нагрузки по таблице
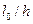
| ||||
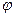
| 0,92 | 0,9 | 0,83 | 0,7 |
при кратковременном действии нагрузки значения 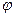 определяют по линей ному закону, принимая
определяют по линей ному закону, принимая 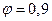 при
при 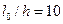 и
и  при
при  ;
;
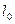 - расчётная длина элемента; в частности, для сборных колонн многоэтажных зданий, кроме колонн первого этажа, она равна
- расчётная длина элемента; в частности, для сборных колонн многоэтажных зданий, кроме колонн первого этажа, она равна 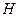 , для сборных колонн первого этажа и монолитных колонн – 0,7
, для сборных колонн первого этажа и монолитных колонн – 0,7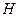 ,
, 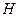 - высота этажа;
- высота этажа;
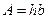 - площадь сечения элемента; для квадратного поперечного сечения
- площадь сечения элемента; для квадратного поперечного сечения 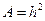 ;
;
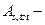 площадь сечения всей продольной арматуры в сечении элемента.
площадь сечения всей продольной арматуры в сечении элемента.
Последовательность расчёта условно центрально сжатого элемента следующая.
· Принять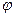 = 1;
= 1; 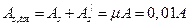 . Здесь
. Здесь 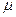 - коэффициент армирования поперечного сечения.
- коэффициент армирования поперечного сечения.
Тогда, заменив в формуле (6.27)усилие  усилием
усилием 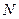 , получим:
, получим:
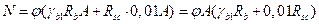 .
. (48*)
(48*)
Отсюда: 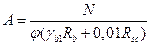 . (49*)
. (49*)
· Вычислить по формуле (49*) при 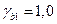 (кратковременное действие нагрузки)
(кратковременное действие нагрузки)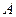 ; по
; по 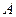 принять размер сечения элемента
принять размер сечения элемента 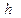 .
.
· По 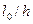 , используя линейную интерполяцию или экстраполяцию, выбрать значение коэффициента
, используя линейную интерполяцию или экстраполяцию, выбрать значение коэффициента 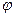 (при кратковременном действии нагрузки).
(при кратковременном действии нагрузки).
· Из формулы (6.27) получаем выражение для определения  :
:
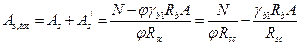 . (50*)
. (50*)
· Вычислить по формуле (50*) при 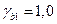
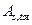 .
.
· Вычислить  . Если
. Если 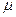 = 0,01…0,02, по сортаменту подобрать необходимое армирование. Если
= 0,01…0,02, по сортаменту подобрать необходимое армирование. Если 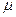
 0,01…0,02, то изменить
0,01…0,02, то изменить 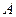 , т.е.
, т.е. 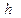 (при
(при 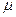 > 0,02 - увеличить, при
> 0,02 - увеличить, при 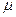 < 0,01 – уменьшить), выбрать новое значение
< 0,01 – уменьшить), выбрать новое значение 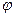 , по формуле (50*) – новую
, по формуле (50*) – новую 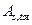 , вычислить новый
, вычислить новый 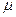 ; если он опять не попал в «вилку» 0,01…0,02, то перерасчёт повторить.
; если он опять не попал в «вилку» 0,01…0,02, то перерасчёт повторить.
· Повторить все вычисления, заменив в формулах (49*) и (50*) усилие 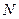 усилием
усилием 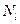 .
.
Вследствие длительного действия нагрузки значение 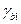 в указанных формулах принять равным 0,9, а значения коэффициента
в указанных формулах принять равным 0,9, а значения коэффициента 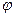 выбирать из вышеприведённой таблицы.
выбирать из вышеприведённой таблицы.
· В качестве расчётного значения симметричной арматуры принять наибольший из двух полученных результатов.
Расчёт внецентренно сжатых элементов прямоугольного сечения.
Эксцентриситет сжимающей силы N относительно продольной геометрической оси элемента 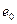 определяют по формуле
определяют по формуле
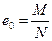 .
. (51*)
(51*)
При гибкости элемента 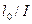 > 14 (где
> 14 (где 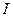 - момент инерции сечения, равный
- момент инерции сечения, равный 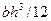 ), полученное по формуле (56*) значение
), полученное по формуле (56*) значение 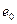 умножают на коэффициент
умножают на коэффициент 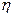 , учитывающий влияние прогиба элемента на его несущую способность и определяемый по формуле
, учитывающий влияние прогиба элемента на его несущую способность и определяемый по формуле
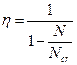 , (6.23)
, (6.23)
где 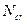 - условная критическая сила, определяемая по формуле
- условная критическая сила, определяемая по формуле
 ,
, (6.24)
(6.24)
здесь 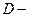 жёсткость элемента, определяемая по формуле
жёсткость элемента, определяемая по формуле
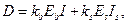 (6.25)
(6.25)
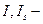 моменты инерции площадей сечения соответственно бетона и всей продольной арматуры относительно центра тяжести поперечного сечения элемента;
моменты инерции площадей сечения соответственно бетона и всей продольной арматуры относительно центра тяжести поперечного сечения элемента;
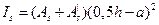 ;
;
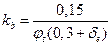 ;
; 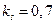 ;
;
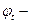 коэффициент, учитывающий влияние длительности действия нагрузки;
коэффициент, учитывающий влияние длительности действия нагрузки;
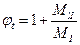 ;
;
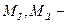 моменты относительно центра тяжести наиболее растянутой или наименее сжатой (при целиком сжатом сечении) арматуры соответственно от действия полной нагрузки и от действия постоянных и временных длительных нагрузок;
моменты относительно центра тяжести наиболее растянутой или наименее сжатой (при целиком сжатом сечении) арматуры соответственно от действия полной нагрузки и от действия постоянных и временных длительных нагрузок;
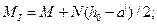
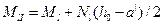 ;
;
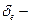 относительное значение эксцентриситета продольной силы, равное
относительное значение эксцентриситета продольной силы, равное 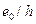 и принимаемое не менее 0,15.
и принимаемое не менее 0,15.
Расстояние от точки приложения силы 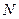 до центра тяжести сечения растянутой или наименее сжатой (при полностью сжатом сечении элемента) арматуры равно
до центра тяжести сечения растянутой или наименее сжатой (при полностью сжатом сечении элемента) арматуры равно
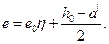 (52*)
(52*)
В зависимости от величины эксцентриситетов 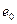 и е различают: случай 1 - случай больших эксцентриситетов и случай 2 – случай малых эксцентриситетов.
и е различают: случай 1 - случай больших эксцентриситетов и случай 2 – случай малых эксцентриситетов.
В случае 1 эксцентриситеты настолько большие, что в части сечения, более удалённой от силы N, возникают значительные растягивающие напряжения, и разрушение элемента происходит аналогично разрушению изгибаемого нормально армированного элемента (см. п. 1.4).
В этом случае выполняется условие 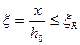 , и предельный момент
, и предельный момент  (рис. 8) определяется по формуле (6.14) (в левой части
(рис. 8) определяется по формуле (6.14) (в левой части 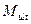 заменяется на
заменяется на  ). Высоту сжатой зоны
). Высоту сжатой зоны  определяют по формуле, аналогичной формуле (6.15):
определяют по формуле, аналогичной формуле (6.15):
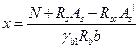 . (6.21)
. (6.21)
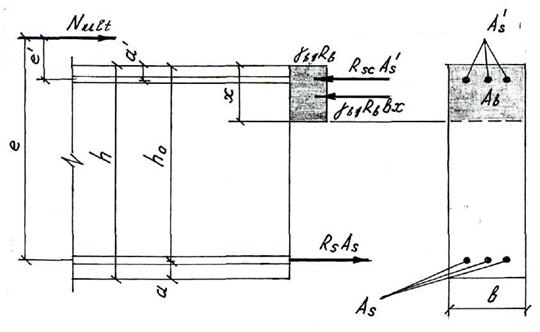
Рис. 8 - Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси
внецентренно сжатого железобетонного элемента, при расчёте его по прочности
В случае 2 эксцентриситеты малы, поэтому часть сечения, более удалённая от силы N, остаётся сжатой или в ней возникают небольшие растягивающие напряжения, и разрушение элемента происходит аналогично разрушению изгибаемого переармированного элемента (см. п. 1.4).
В этом случае выполняется условие 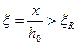 , и разрушающий момент
, и разрушающий момент  (рис. 8) определяется также по формуле (6.14) (в левой части
(рис. 8) определяется также по формуле (6.14) (в левой части 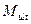 заменяется на
заменяется на ), но подставляют в неё значение
), но подставляют в неё значение  , определённое по формуле
, определённое по формуле
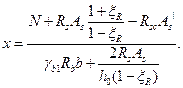 (6.22)
(6.22)
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 3662; Нарушение авторских прав?; Мы поможем в написании вашей работы!