Решение позиционных задач в аксонометрии

Алгоритмы решения позиционных задач на аксонометрическом чертеже не отличаются от алгоритмов решения этих задач в ортогональных проекциях на эпюре Монжа.

Пример. Построить следы прямой l (рис. 13.9).

Решение. Алгоритм решения задачи такой же, как и на эпюре Монжа.

T – фронтальный след прямой l, K – горизонтальный след и E – профильный след (рис.13.9).

Рис. 13.9

Рассмотрим примеры построения пересечения геометрических фигур в аксонометрии.

Пример. Построить пересечение заданной прямой l и плоскости Г(АВС) (рис. 13.10).

Решение.

Плоскость Г(АВС) и прямая l заданы своими аксонометрическими и вторичными проекциями. Задачу решаем, используя вспомогательную плоскость-посредник.

1. Заключаем прямую l во вспомогательную вертикальную плоскость å. При этом å₁¢, совпадающая с l₁¢, представляет собой вторичную проекцию вертикальной плоскости-посредника. Отметим, что вторичная проекция любой фигуры, расположенной в плоскости å, совпадает с вторичной проекцией å ₁ ¢.

2. Строим пересечение заданной плоскости Г(АВС) с плоскостью-посредником å; во-первых находим точки пересечения вторичных проекций плоскостей (å₁¢ ∩ A₁¢B₁¢C₁¢ = 1₁¢ 2₁¢); затем проводим вертикальные линии связи из 1₁¢ и 2₁¢ до пересечения с аксонометрическими проекциями соответствующих сторон заданной плоскости, а именно 1¢ и 2¢. Объединяем точки в прямую 1¢ 2¢.

3. Определяем точку Т¢ пересечения прямой l' и плоскости A¢B¢C¢, а именно l' ∩ 1¢ 2¢ = Т¢. По принадлежности к l₁¢, находим вторичную проекцию точки пересечения Т₁¢.

4. Для определения видимости прямой относительно заданной плоскости воспользуемся конкурирующими точками 3 и 4, принадлежащими соответственно заданной прямой и стороне ВС плоскости. Проведя линии связи, определяем вторичные проекции выбранных точек. По положению вторичных проекций определяем видимость заданной прямой относительно плоскости.

Рис. 13.10

Пример. Построить пересечение прямой l и конической поверхности Δ (рис. 13.11).

Рис. 13.11

Пример. Построить пересечение призмы и плоскости Г (рис. 13.12).

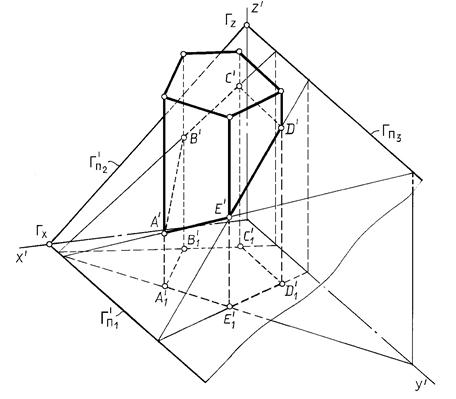
Рис. 13.12

Пример. Построить пересечение цилиндра и плоскости Σ (рис. 13.13).

Рис. 13.13

Пример. Построить пересечение призмы и цилиндра (рис. 13.14).

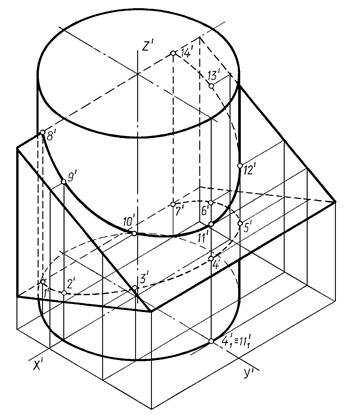
Рис. 13.14

Лекция 14

Проекции с числовыми отметками

Проекции точки. Проекции прямой. Градуирование прямой. Взаимное положение двух прямых. Плоскость. Проекции поверхностей.

При проектировании инженерно-строительных сооружений приходится прибегать к изображению земной поверхности. Форма поверхности земли и земляных сооружений – сложна, а их вертикальные размеры по отношению к горизонтальным очень малы, например: дороги, мосты, аэродромы, строительные площадки, гидротехнические объекты и т.д. Для их изображения на строительных чертежах существует специальный метод – проекции с числовыми отметками.

Дата добавления: 2014-01-05