Поверхностей

Пересечение двух плоскостей, плоскости и поверхности, двух

С числовыми отметками

Построение пересечения геометрических фигур в проекциях

Так как каждая из поверхностей (в том числе и плоскость) изображается при помощи семейства горизонталей, то линия пересечения поверхностей (плоскостей) может быть построена как множество точек пересечения с одинаковыми отметками.

Рассмотрим примеры построения линий пересечения различных геометрических фигур в проекциях с числовыми отметками.

Пример. Построить линию пересечения плоскостей Г и ∆, заданных масштабами уклонов (рис. 15.1).

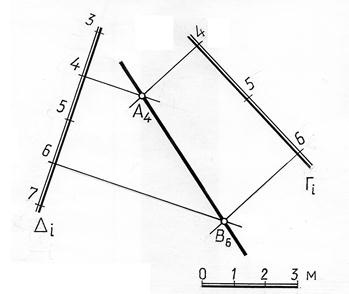
Рис. 15.1

Решение. Так как линия пересечения плоскостей – прямая, то для её построения достаточно найти точки пересечения двух пар одинаковых по высоте горизонталей, например, горизонталей 5 и 7. Точки А₅ и В₇ определяют прямую АВ, которая является линией пересечения заданных плоскостей.

Пример. Построить линию пересечения плоскостей Г и ∆, заданных масштабами уклонов, при условии, что горизонтали этих плоскостей параллельны (рис. 15.2).

Решение. Горизонтали заданных плоскостей параллельны, но сами плоскости не параллельны, так как не равны интервалы и, следовательно, углы наклона к плоскости проекций.

Рис. 15.2

Горизонтали заданных плоскостей параллельны, следовательно, параллельны их горизонтальные следы, которые являются нулевыми горизонталями. Если две плоскости пересекают третью (П₀) по параллельным прямым, то и линия пересечения этих плоскостей будет параллельна этой плоскости.

Следовательно, линия пересечения заданных плоскостей параллельна плоскости П₀, т. е. является их горизонталью.

Для определения точки, через которую пройдёт искомая линия пересечения заданных плоскостей, проведена вспомогательная плоскость å. Эта плоскость задана произвольным масштабом уклонов å_i. Затем построены линии пересечения заданных плоскостей со вспомогательной плоскостью å. Горизонтали этих плоскостей пересекаются, поэтому нетрудно построить их линии пересечения:

А₅В₆ – линии пересечения плоскостей Δ и å;

С₆К₅ – линия пересечения плоскостей Г и å,

Точка Т_5,3 пересечения линий А₅В₆ и С₆К₅ принадлежит всем трём плоскостям, а следовательно, линии пересечения заданных плоскостей.

Аналогично решается задача, если горизонтали заданных плоскостей не параллельны, но пересекаются за пределами чертежа. Так как в этом случае направление линии пересечения неизвестно, то вводятся две вспомогательные плоскости и определяются две точки. принадлежащие искомой линии пересечения плоскостей.

Пример. Построить линию пересечения топографической поверхности горизонтально проецирующей (вертикальной) плоскостью А (рис.15.3).

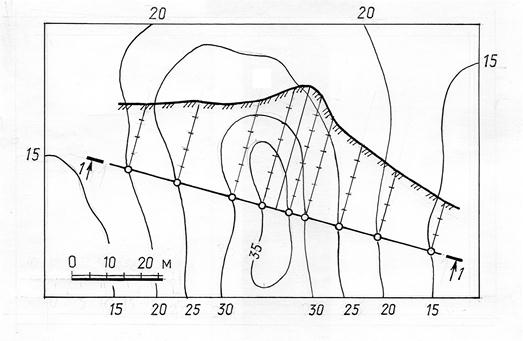
Рис. 15.3

Сечение топографической поверхности вертикальной плоскостью называется профилем поверхности. Профиль может изображаться на свободном месте чертежа (вынесенный профиль) или совмещаться с чертежом топографической поверхности (наложенный профиль).

Решение. Для построения наложенного профиля (рис. 15.3) определяются точки пересечения проекции заданной плоскости (линии 1-1) с горизонталями топографической поверхности, затем из этих точек проводятся перпендикуляры к линии 1-1. на которых в масштабе чертежа откладываются превышения точек пересечения над выбранной линией уровня – базы профиля. Плавная линия, соединяющая построенные точки, и есть профиль топографической поверхности.

На рис. 15.4 показано построение вынесенного профиля той же топографической поверхности. Для построения вынесенного профиля вычерчивается линия - база профиля и вертикальная линия, задающая вертикальный масштаб. На базу профиля с плана (см. рис. 15.3) переносятся заложения, определяющие точки пересечения горизонталей топографической поверхности с заданной плоскостью. Из полученных точек восстанавливаются перпендикуляры к базе профиля до пересечения с горизонтальными линиями, имеющими такие же числовые отметки. Полученные таким образом точки соединяются плавной линией, которая образует профиль сечения.

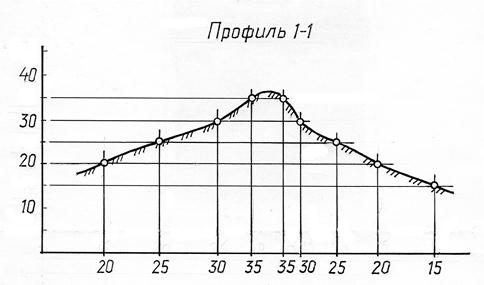
Рис. 15. 4

Пример. Построить линию пересечения топографической поверхности наклонной плоскостью (рис. 15.5).

Рис. 15.5

Решение. Линия пересечения топографической поверхности плоскостью проходит через точки пересечения их горизонталей с одинаковыми отметками. Соединяя плавной линией построенные точки, получим искомую линию пересечения.

Выполненные построения ясны из чертежа.

Если горизонтали топографической поверхности и плоскости в пределах чертежа не пересекаются (или не пересекаются вообще), можно применить известный метод вспомогательных секущих плоскостей (см. рис.15.2). На рис.15.6 показано построение линий пересечения топографической поверхности с плоскостью Г, горизонтали которых не пересекаются. Для этого проведены две вспомогательные плоскости å и ∆. Плоскость å пересекает топографическую поверхность по линии А₂₄ В₂₃ (дуга линии пересечения заменена отрезком прямой для упрощения). Эта же плоскость пересекает заданную плоскость по прямой С₂₃ К_24. Точка Т_23,5 пересечение прямых А₂₄В₂₃ и С₂₃К₂₄ – принадлежит линии пересечения топографической поверхности и плоскости Г. Аналогично строится точка искомой линии пересечения – точка М_23,4. В зависимости от требуемой точности можно построить любое количество точек, принадлежащих линии пересечения.

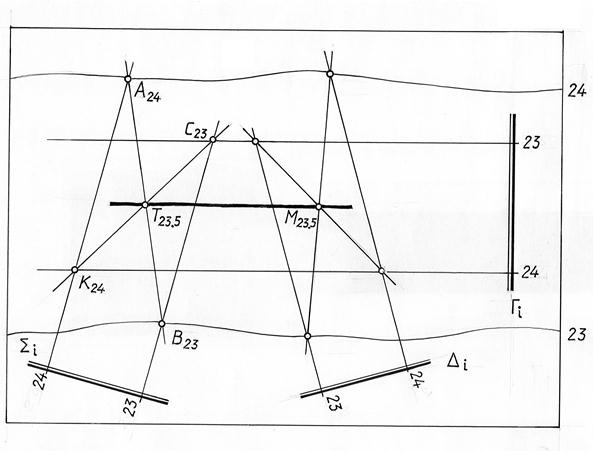
Рис. 15.6

На рис. 15.7 показано решение этой же задачи с использованием вспомогательных секущих вертикальных плоскостей (метод профилей). Заданная топографическая поверхность и плоскость Г пересечены двумя вспомогательными горизонтально проецирующими плоскостями å и ∆, и построены профили сечения этими плоскостями.

При построении профиля вертикальные масштабы выбраны произвольно и для упрощения дуги линий, по которым вспомогательные плоскости пересекают топографическую поверхность, заменены отрезками прямых. Все построения ясны из чертежа.

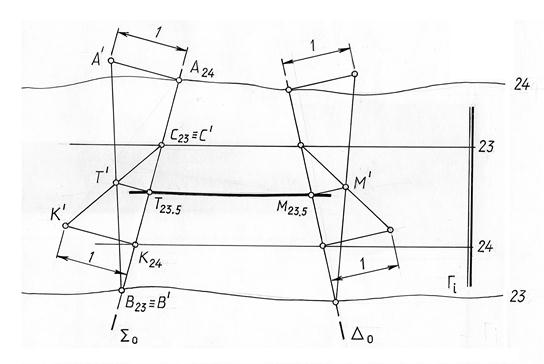
Рис. 15.7

Пример. Построить линию пересечения топографической и конической поверхностей (рис. 15.8).

Решение. Построение линии пересечения поверхностей сводится к нахождению точек пересечения их горизонталей, имеющих одинаковые отметки.

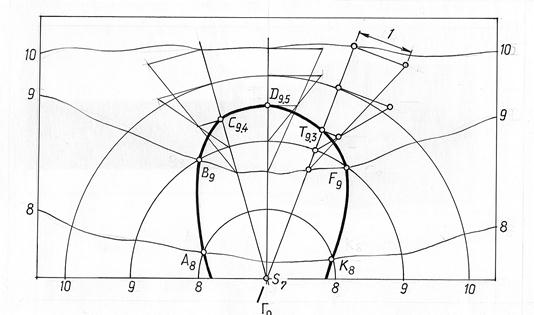
Рис. 15.8

Для определения точки Т, принадлежащей линии пересечения и находящейся между горизонталями 9 и 10, использована вспомогательная вертикальная плоскость Г. Построены профили сечения топографической и конической поверхностей плоскостью Г (условно кривые заменены отрезками прямых).

Дата добавления: 2014-01-05