
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 8. Шифрование сообщений
|
|
|
|
Магические квадраты
Тюремный шифр
Квадрат Полибия
Книжный шифр
Шифр Гай Юлия Цезаря
Основные положения.
Шифрование сообщений
Лекция 7
Q
Q
А
В
А
Элемент
В логический
Ввод
Рассмотрим логическую схему для операторов И, ИЛИ, and НЕ: (А V ØВ) & (ØА V В)
 В
В
| Конъюнкция | Дизъюнкция | Инверсия | ||||||||
 0 0 0 0
|
 
|
| ||||||||

|
|
| ||||||||
|
|
Переменным, входящим в состав выражения, соответствуют линии-входы. Значению выражения соответствует линия-выход. Иногда на выходе схемы бывает нужно узнать не только значение выражения, но и значения его отдельных частей. В таких случаях у схемы бывает несколько линий-выходов.
Для иллюстрации действия логических функций, можно использовать другие логические схемы, где 1 -ИСТИНА и 0-ЛОЖЬ.
Еще в 1910 году физик П.С. Эренфест указал на возможность использования аппарата логики для работы релейно-контактных схем, в связи с тем, что каждой схеме можно поставить в соответствие некоторую формулу алгебры логики и каждая формула алгебры логики реализуется с помощью некоторой схемы. Эти устройства (их часто называют переключательными или коммутационными схемами) содержат сотни реле, полупроводниковых элементов и других переключающих элементов.
Под переключательной схемой понимается схематическое изображение некоторого устройства, состоящего из:
-переключателей
-соединительных проводников
-входов в схему и выходов из нее
Коммутационной схемой принимается в расчет только два состояния каждого переключателя, которые называются «замкнутым» и «разомкнутым»
Рассмотрим схему переключателя, состоящую из источника питания и электрической лампочки.
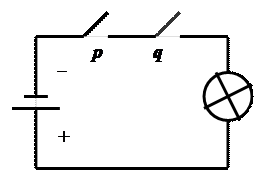
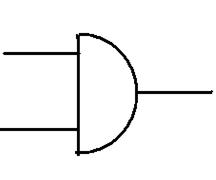 Присвоим значение 1 переключателям p и q если они замкнуты (т.е. если через них проходит ток. В противоположной ситуации (т.е. когда они разомкнуты и ток через них не проходит) присвоим им значение 0.Присвоим значение 1 схеме, когда лампочка светится (т.е. электрический ток через нее проходит. Понятно, что лампочка загорится, тогда и только тогда, когда оба переключателя замкнуты, т.е. когда p и q имеют значение 1. Таким образом, схема соответствует высказыванию p & q. Такое расположение переключателей называется логическим элементом p и q или схемой логического умножения. Этот логический элемент обозначается следующим символом и называется элементом логического умножения.
Присвоим значение 1 переключателям p и q если они замкнуты (т.е. если через них проходит ток. В противоположной ситуации (т.е. когда они разомкнуты и ток через них не проходит) присвоим им значение 0.Присвоим значение 1 схеме, когда лампочка светится (т.е. электрический ток через нее проходит. Понятно, что лампочка загорится, тогда и только тогда, когда оба переключателя замкнуты, т.е. когда p и q имеют значение 1. Таким образом, схема соответствует высказыванию p & q. Такое расположение переключателей называется логическим элементом p и q или схемой логического умножения. Этот логический элемент обозначается следующим символом и называется элементом логического умножения.
p
p & q
Теперь рассмотрим схему, когда переключатели соединены в схеме параллельно
|

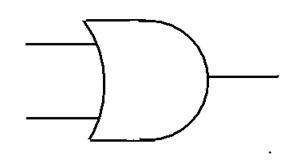
Понятно, что лампочка загорается и значение схемы становится равным 1. когда один из двух переключателей замкнут, то есть либо p =1, либо q =1, либо они оба равны 1. Эта схема соответствует высказыванию p V q и называется логическим элементом p или q, или схемой логического сложения и изображается символом.
 p
p
p V q
Предположим, имеется схема с одним переключателем p, который обладает таким свойством, что лампочка загорается тогда и только тогда, когда переключатель разомкнут. Следовательно, схема имеет значение 1, когда p равно 0, и, наоборот, значение 0, когда p равно 1. Эта схема соответствует 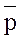 , а соответствующий логический элемент называется логическим элементом не, или инвертором.
, а соответствующий логический элемент называется логическим элементом не, или инвертором.

P 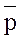
Из трех логических элементов, соответствующих выражениям сложения, умножения и отрицания, можно строить электронные логические схемы любой сложности. Например, представленную ниже схему (p v q) & .
.
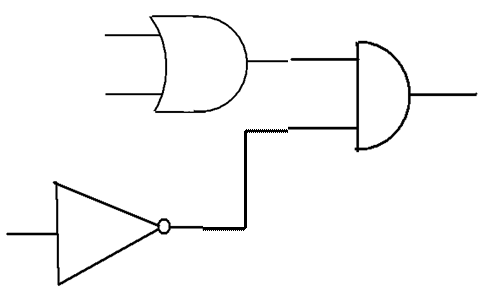
(p v q) &
Существовали три основных способа защиты информации.
Первый способ предполагает чисто силовые методы: охрана документа (носителя информации) физическими лицами, его передача специальным курьером и т. д.
Второй способ получил название "стеганография" и заключается в сокрытии самого факта наличия секретной информации. В этом случае, в частности, использовались невидимые, так называемые “симпатические чернила”. При соответствующем проявлении текст становится видимым. Один из оригинальных примеров сокрытия информации приведён в трудах древнегреческого историка Геродота. На голове раба, которая брилась наголо, записывалось нужное сообщение. И когда волосы его достаточно отрастали, раба отправляли к адресату, который снова брил ему голову и считывал полученное сообщение.
Во время II Мировой войны похожими методами иногда передавались агентурные сообщения. Секретные послания записывались симпатическими чернилами на предметах нижнего белья, носовых платках, галстуках
и т. д. В настоящее время под стеганографией чаще всего понимают сoкрытие информации в текстовых, графических либо аудио файлах путём использования специального программного обеспечения.
Третий способ защиты информации заключается в преобразовании смыслового текста в некий хаотический набор знаков (букв алфавита). Получатель донесения имеет возможность преобразовать его в исходное осмысленное сообщение, если обладает «ключом» к его построению. Этот способ защиты информации называется криптографическим.
Криптография - это процесс преобразования сообщения в секретный код и обратное преобразование закодированного сообщения снова в первоначальный текст.
Первоначальное преобразование называется шифрованием.
Шифрова́ние — способ преобразования открытой информации в закрытую и обратно. Применяется для хранения важной информации в ненадёжных источниках или передачи её по незащищённым каналам связи.
Незакодированное сообщение называют «открытый текст». Закодированное сообщение называется «зашифрованный текст». Дешифрование конвертирует (преобразовывает) зашифрованный текст назад в открытый текст. Во времена холодной войны, криптография была областью военных и разведывательных служб; а «невзламываемые» коды резервировали только для сотрудников секретных служб. Без криптографии люди не могут быть уверены, что электронные финансовые сделки, секретные или частные данные и ценная интеллектуальная собственность останутся конфиденциальными при передаче по электронной сети. Организации шифруют текст и видеозаписи проводимых телеконференций. Индивидуумы кодируют свою электронную почту. Исследователи используют шифрование, чтобы скрыть информацию о новых открытиях от любопытных глаз.
Криптосистема - пакет программ, который использует алгоритм или математическую формулу, плюс ключ, чтобы зашифровать и дешифровать сообщения. Алгоритм рассчитывается с помощью ключа и конвертирует каждый знак открытого текста в другие закодированные знаки, таким образом, создавая зашифрованный текст. Только обладатель соответствующего ключа способен расшифровать шифровку. Хорошо зашифрованный текст кажется ничем иным, как случайным набором чисел. Шифрование делает информацию бесполезной хакерам и ворам.
В криптографии с древних времен использовались два вида шифров: замена и перестановка.
Историческим примером шифра замены является шифр Цезаря. Цезарь использовал в своей переписке шифр собственного изобретения. Применительно к современному русскому языку он состоял в следующем. Выписывался алфавит: А, Б, В, Г, Д, Е,...; затем под ним выписывался тот же алфавит, но с циклическим сдвигом на 3 буквы влево:
А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Ъ Ь Э Ю Я
А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ ЫЪ Ь Э Ю Я А Б В
При шифровании буква А заменялась буквой Г, Б заменялась на Д, В – Е и так далее. Получатель сообщения искал эти буквы в нижней строке и по буквам над ними восстанавливал исходное слово. Ключом в шифре Цезаря является величина сдвига 2-й нижней строки алфавита. Преемник Цезаря – Цезарь Август использовал тот же шифр, но с ключом – сдвиг на 1 позицию.
Естественное развитие шифра Цезаря очевидно: нижняя строка двухстрочной записи букв алфавита может быть с произвольным расположением этих букв. Если в алфавитном расположении букв в нижней строке существует всего 33 варианта ключей (число букв в русском алфавите), то при их произвольном расположении число ключей становится огромным. Оно равно 33! (33 факториал), т.е. приблизительно десять в тридцать пятой степени! Этот момент очень важен. Если противник догадался или получил сведения об используемом шифре (а шифры используются длительное время), то он может попробовать перебрать все варианты возможных секретных ключей при дешифровании перехваченной криптограммы. В современных условиях такой перебор в шифре Цезаря производится за несколько минут. Но перебор 33! Он занял бы несколько столетий.
Рассмотрим пример шифра перестановки. Выберем целое положительное число, скажем 5; расположим числа от 1 до 5 в двухстрочной записи, в которой вторая строка – произвольная перестановка чисел верхней строки:
Зашифруем фразу "СВЯЩЕННАЯ РИМСКАЯ ИМПЕРИЯ". В этой фразе 23 буквы.
Дополним её двумя произвольными буквами (например, Ь, Э) до ближайшего числа, кратного 5, то есть 25. Выпишем эту дополненную фразу без пропусков, одновременно разбив её на пятизначные группы:
СВЯЩЕ ННАЯР ИМСКА ЯИМПЕ РИЯЬЭ
Буквы каждой группы переставим в соответствии с указанной двухстрочной записью по следующему правилу: первая буква встаёт на третье место, вторая – на второе, третья – на пятое, четвёртая – на первое и пятая – на четвёртое. Полученный текст выписывается без пропусков:
ЩВСЕЯЯННРАКМИАСПИЯЕМЬИРЭЯ
При дешифровании текст разбивается на группы по 5 букв и буквы переставляются в обратном порядке: 1 на 4 место, 2 на 2, 3 на 1, 4 на 5 и 5 на 3. Ключом шифра является выбранное число 5 и порядок расположения чисел в нижнем ряду двухстрочной записи.
Было предложено прокалывать малозаметные дырки в книге или в другом документе над буквами секретного сообщения. Интересно отметить, что в первой мировой войне германские шпионы использовали аналогичный шифр, заменив дырки на точки, наносимые симпатическими чернилами на буквы газетного текста.
Книжный шифр в современном его виде имеет несколько иной вид. Суть этого шифра состоит в замене букв на номер строки и номер этой буквы в строке в заранее оговоренной странице некоторой книги. Ключом такого шифра является книга и используемая страница в ней.
Полибий – греческий государственный деятель, полководец, историк, III век до н. э. Применительно к современному латинскому алфавиту из 26 букв, шифрование по этому квадрату заключалось в следующем. В квадрат размером 5x5 клеток выписываются все буквы алфавита, при этом буквы I, J не различаются:

| A | B | C | D | E |
| A | A | B | C | D | E |
| B | F | G | H | I | K |
| C | L | M | N | O | P |
| D | Q | R | S | T | U |
| E | V | W | X | Y | Z |
Шифруемая буква заменялась на координаты квадрата, в котором она записана. Так, B заменялась на AB, F на BA и т. д. При дешифровании каждая такая пара определяла соответствующую букву сообщения. Заметим, что секретом в данном случае является сам способ замены букв. Ключ в этой системе отсутствует, поскольку используется фиксированный алфавитный порядок следования букв.
Усложненный вариант шифра Полибия заключается в записывании в квадрат букв в произвольном (неалфавитном) порядке. Этот произвольный порядок является ключом.
В несколько изменённом виде шифр Полибия дошёл до наших дней и получил своеобразное название "тюремный шифр". Для его использования нужно знать естественный порядок расположения букв алфавита. Стороны вышерассмотренного квадрата обозначаются не буквами (ABCDE), а числами (12345). Число 3, например, передаётся путём тройного стука. При передаче буквы сначала "отстукивается" число, соответствующее строке, в которой находится буква, а затем номер соответствующего столбца. Например, буква "F" передаётся двойным стуком (вторая строка) и затем одинарным (первый столбец).
"Тюремный шифр", строго говоря, не шифр, а способ перекодировки сообщения с целью его приведения к виду, удобному для передачи по каналу связи (через стенку).
Во времена средневековья криптографию, в какой то степени, отождествляли с черной магией, с некоторой формой оккультизма, астрологией и алхимией. К шифрованию информации призывались мистические силы. Так, например, рекомендовалось использовать "магические квадраты".
В квадрат размером 4 на 4 (размеры могли быть и другими) вписывались числа от 1 до 16. Его магия состояла в том, что сумма чисел по строкам, столбцам и полным диагоналям равнялась одному и тому же числу – 34. Впервые эти квадраты появились в Китае.
Шифрование по магическому квадрату производилось следующим образом.
| 16 У | 3 И | 2 Р | 13 Д |
| 5 З | 10 Е | 11 Г | 8 Ю |
| 9 С | 6 Ж | 7 А | 12 О |
| 4 Е | 15 Я | 14 Н | 1 П |
Например, требуется зашифровать фразу: "Приезжаю сегодня". Буквы этой фразы вписываются последовательно в квадрат согласно записанным в них числам, а в пустые клетки ставятся произвольные буквы. После этого шифрованный текст записывается в строку:
УИРДЗЕГЮСЖАОЕЯНП
При расшифровывании текст вписывается в квадрат, и открытый текст читается в последовательности чисел "магического квадрата". Данный шифр – обычный шифр перестановки.
Решетка Кардано
Из плотного материала вырезался прямоугольник размером, например, 7 x 10; в нем проделывались окна (на рисунке они заштрихованы).
Секретный текст вписывался в эти окна, затем решетка снималась и оставшиеся клетки старались заполнить так, чтобы получалось "невинное" сообщение.
Такого рода шифр использовал известный русский писатель, общественный деятель и дипломат А. С. Грибоедов. Будучи послом в Персии, он писал своей жене "невинные" послания, которые, попав в руки жандармерии, для которой и были предназначены, расшифровывались по соответствующей "решетке" и передавались царскому правительству уже как секретные сведения.
Шифрование используется не только для хранения секретов. Оно может использоваться, чтобы проверить, кто послал сообщение и сообщить, вносили ли изменения в сообщение при передаче. Цифровая (электронная) подпись - технология, которая используется для исполнения вышеназванных нужд при проведении финансовых сделок он-лайн. Цифровые подписи требуют применения сложной технологии, которая объединяет ключевой метод шифрования со смешанным алгоритмом. Смешанный алгоритм обеспечивает шифрование, преобразовывая набор знаков в другой набор (например, буква f преобразовывается в g, 3 в 8 и т.д.). Таким образом, шифрование может предотвращать электронное мошенничество, подтверждая подлинность цифровой подписи отправителя.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1009; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 0
0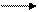
 0 1
0 1

 1
1
 1 0
1 0

 1 1
1 1

 1 1 1
1 1 1