Поиск решения. Существует множество задач, которые нельзя решить с помощью средства Подбор параметра

Существует множество задач, которые нельзя решить с помощью средства Подбор параметра. Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решения. В этом случае необходимо использовать надстройку Поиск решения.

Программа Поиск решения позволяет анализировать оптимальные задачи трех типов:

· Линейные,

· Нелинейные,

· Целочисленные.

Задачи оптимизации.

Слова оптимум, оптимальный происходят от латинского орtimus, означающего наилучший.

В повседневной жизни мы сталкиваемся с необходимостью решать оптимальные задачи. Так каждый раз, когда мы заходим в магазин, перед нами встает одна и та же проблема, как максимально удовлетворить потребности, соизмеряясь с возможностями нашего кошелька. Но можно решать и другую задачу, как истратить его содержимое – купив как можно больше вкусных вещей. Что же говорить об инженера, экономистах, менеджерах, которые постоянно сталкиваются с разнообразными проблемами.

Оптимизация технических и управленческих решений вызвана необходимостью экономить энергию, материалы, время, трудовые ресурсы. Даже небольшая (в несколько процентов) экономия энергии и ресурсов приводит к существенному экономическому эффекту в рамках предприятия, отрасли и страны.

Чтобы понять суть задачи оптимизации вначале остановимся на самом простом примере.

Необходимо спроектировать бак, имеющий форму прямоугольного параллелепипеда, объем которого

где а, в, с - стороны бака.

Требуется определить размеры бак, объемом 2000, чтобы на его изготовление пошло как можно меньше материала, площадь которого

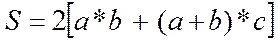
Т.е. нам необходимо минимизировать величину S при условии, что V=2000

Или

Z=S = 2*[a*b+(a+b)*с] Þmin,

a*b*с=2000

К этому очевидно стоит добавить очевидное, что все стороны прямоугольника должны быть положительны,

т.е. а,b,с>0.

Если обозначим через х₁ =а, х₂ =b, х₃ =с, тогда

Z=2*[x₁ *x₂ +(x₁ + x₂ )*x₃ ]Þmin

x₁* x₂* x₃= 2000

x₁, x₂, x₃>0

В общем случае задача оптимизации запишется в следующем виде:

Здесь

Ø ЦФ – целевая функция или критерий оптимизации показывает, в каком смысле решение должно быть оптимальным, т.е. наилучшим. При этом возможны 3 вида назначения целевой функции
·максимизация
·минимизация
·назначение заданного значения

Ø ОГР – ограничения устанавливают зависимости между переменными. Они могут быть

·как односторонние

·так и двухсторонние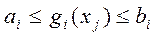

Ø ГРУ – граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.

Решение задачи, удовлетворяющее всем ограничениям и граничным условиям, называется допустимым.

Если целевая функция Z и система функций ограничений линейны относительно входящих в задачу неизвестных х_j, то такой раздел математического программирования называется линейным программированием.

Если в задаче математического программирования целевая функция и (или) хотя бы одна из функций системы ограничений нелинейна, то такой раздел называется нелинейным программированием.

Если на все или некоторые переменные х_j наложено условие целочисленности, то такие задачи относятся к задачам целочисленного (дискретного) программирования.

Рассмотрим элементы диалогового окна Поиск решения. Для этого зайдем в Сервис, Поиск решения. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис отсутствует команда Поиск решения, то для установки необходимо выполнить команду Сервис, Надстройки, Поиск решения.

Рисунок - Элементы диалогового окна «Поиск решения»

Дата добавления: 2014-01-05