Вводные определения и понятия

Данные и знания не всегда бывают точными и полностью достоверными. При этом существует довольно широкий класс процессов (в образовании, экономике, промышленности, экологии, военном деле и др.), управление которыми формируется на основе знаний, обладающих неопределенностью. Более того, данные нейропсихологии свидетельствуют о том, что объекты окружающего мира в памяти мозга адекватно распознаются и фиксируются по неполной информации [9].

Человек использует нечеткие представления для оценки физических величин, состояний объектов и систем на приближенном, качественном уровне. Будем называть высказывание нечетким, если его истинность (или ложность) не может быть установлена с определенностью. Отметим, что качественная оценка имеет нечисловой характер, поскольку не обладает свойством аддитивности, присущим числам.

Формализация качественных оценок проводится на основе теории нечетких множеств [10], созданной Л. Заде в 1965 г. в США [11]. Рассмотрим основные понятия, связанные с нечеткими множествами.

Лингвистическойпеременной является переменная, определяемая лингвистическими значениями, выражающими те или иные качественные оценки. Например, длина отрезка, скорость автомобиля, напряжение сети и т.п. Лингвистическое значение – это значение лингвистической переменной, выраженное в словесной форме. Например, большой, средний, малый; молодой, старый; приятный, неприятный и т.п. Лингвистическое значение всегда присутствует в модели вместе со связанной с ним лингвистической переменной. Например, высокое давление, прочная конструкция, ранний период и т.п. По этой схеме вводится понятие нечеткого числа, например, около 0, примерно 5, немного более 9, приблизительно между 10 и 12 и т.п.

Поскольку нечеткость часто путают с вероятностью, следует коснуться различий между этими понятиями. Всякий новый объект в процессе познания по отношению к субъекту всегда имеет некоторую неопределенность, которую субъект должен постичь, чтобы получить более-менее адекватное представление о данном предмете. До недавнего времени знание о неопределенности, главным образом, формировалось в рамках теории вероятностей и такую неопределенность называют стохастической неопределенностью [12]. Примером стохастической неопределенности может служить утверждение:

Вероятность выиграть главный приз в лотерее «6 из 49» равно 1/13983816.

Действительно, данная вероятность определяется соотношением:

р = (=.

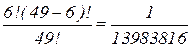
В этом случае стохастическая неопределенность проявляется в виде возникновения конкретного,точно определенного события, состоящего в правильном угадывании шести номеров лотереи.

После знаменитой работы Л.Заде [11] стало очевидным, что рамки одной только стохастической неопределенности явно ограничены, поскольку существует широкий круг неопределенностей, которые не укладываются в концепции теории вероятностей, но описываются в рамках концепции так называемой лексической (лингвистической) неопределенности. Примером лексической неопределенности служит следующее утверждение:

Вероятность выиграть большую сумму в лотерее «6 из 49» мала.

В этом утверждении присутствуют два понятия (большая сумма выигрыша и малая вероятность), которые являются типичными нечеткими понятиями, выраженные лингвистическими переменными с данными лингвистическими значениями. Большинство играющих в лотерею мало задумывается о точном значении вероятности выигрыша, оценивая данную величину интуитивно, по степени своей уверенности в выигрыше: у кого эта степень высокая в лотерее участвует, а у кого низкая – отказывается от участия.

Из этих примеров видно, что нехватка точной информации об объекте не является препятствием для деятельности человека и принятия им решения.

Тем не менее, человек способен эффективно моделировать, как свою деятельность, так и работу механизмов или систем, действуя в рамках нечетких лексических понятий (вроде больше – меньше, лучше – хуже, высокий – низкий и т.п.). При этом, чем шире словарный запас, тем точнее формулировки, используемые при описании рассматриваемых объектов.

Резюмируя, следует сказать, что:

стохастическая неопределенность означает неопределенность в появлении события, которое является само по себе точно описанным;

лексическая неопределенность означает неопределенность в описании события.

Различие между нечеткостью и вероятностью особенно хорошо видно из следующих соображений [13].

Пример. Пусть Х – множество всех жидкостей, А;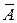 – множества жидкостей, соответственно, пригодных не пригодных для питья, Степень принадлежности ключевой воды множеству А равна 1, множеству 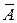равна 0. Пусть речную воду можно отнести к питьевой со степенью 0,6, а к не питьевой – со степенью 0,4 и пусть сосуд С наполнен этой водой.

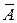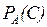Степень принадлежности соляной кислоты множеству А равна 0, а степень принадлежности множеству равна 1. Пусть мы извлекли сосуд Д из корзины, содержащей 10 сосудов, 6 из которых наполнены ключевой водой, а остальные 4 – соляной кислотой. Вероятность извлечь сосуд с ключевой водой, очевидно, равна 0,6. Пусть предстоит выбрать один из следующих сосудов: сосуд С: = 0,6 или сосуд Д: = 0,6. Что бы Вы выбрали, если – степень принадлежности содержимого сосуда С множеству А, 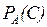– вероятность извлечения сосуда с питьевой водой?

Дата добавления: 2014-01-05