Расчет деревянных элементов на поперечный изгиб

Расчет ведется на прочность и жесткость. Расчет на прочность выполняется по формуле

,

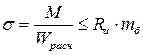где 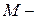расчетный изгибающий момент; расчетное сопротивление древесины изгибу с учетом всех необходимых коэффициентов условий работы; 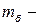коэффициент условий работы, учитывающий размеры поперечного сечения; расчетный момент сопротивления поперечного сечения элемента, равный , если есть ослабления в расчётном сечении. В этом случае определяется с учетом всех ослаблений на участке дайной .

Расчет производится для сечений с максимальным моментом и для сечений с наибольшим количеством ослаблений.

Расчет на устойчивость плоской формы деформирования изгибаемых элементов прямоугольного постоянного сечения производится по формуле

,

где 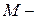расчетный изгибающий момент; 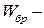максимальный момент сопротивления брутто; 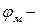коэффициент устойчивости изгибаемых элементов.

Коэффициент 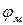для изгибаемых элементов прямоугольного сечения, шарнирно закрепленных от смещения из плоскости изгиба и закрепленных от поворота вокруг продольной оси в опорных сечениях равен

,

где 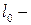расстояние между опорами элемента, а при наличии раскреплений сжатой кромки элемента в промежуточных точках от смещения из плоскости изгиба, 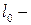расстояние между этим точками;

ширина и максимальная высота сечения элемента на участке ;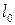

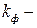коэффициент, зависящий от формы эпюры изгибающего момента на расчетной длине 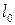, определяемый по табл. СНиП II-25-80.

При расчете изгибаемых элементов с меняющейся по длине высотой и постоянной шириной поперечного сечения коэффициент 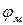, дополнительно умножается на коэффициенты и . Значения приведены в табл. СНиП II-25-80, а находится по формуле

,

где центральный угол в радианах, определяющий 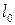элемента кругового очертания (для прямолинейных элементов );

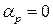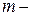число промежуточных подкрепленных точек растянутой кромки на участке 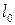[при величину следует принимать равной 1]

Проверку устойчивости плоской формы деформирования изгибаемых элементов двутаврового и коробчатого сечения следует принимать в тех случаях, когда 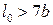, где 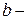ширина сжатого пояса поперечного сечения. Расчет производится по формуле

,

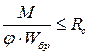где коэффициент продольного изгиба из плоскости изгиба сжатого пояса, определяется как для сжатых элементов;

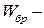момент сопротивления брутто поперечного сечения; в случае фанерных стенок - приведенный момент сопротивления в плоскости изгиба элемента. При поперечном изгибе необходима проверка скалывающих напряжений, определяемых по формуле Журавского

,

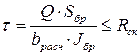где расчетная поперечная сила;

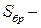статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси;

момент инерции брутто поперечного сечения элемента относительно нейтральной оси;

расчетная ширина поперечного сечения элемента;

расчетное сопротивление древесины скалыванию вдоль волокон при изгибе с учетом всех необходимых коэффициентов условия работы.

Рассмотрим деревянный элемент прямоугольного сечения с размерами 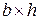, нагруженный равномерно распределенной нагрузкой .

Тогда ; ; ; ; .

; ;

; ;

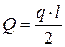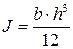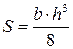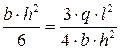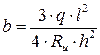
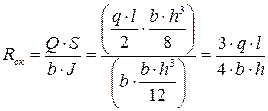Т.е можно табулировать отношение 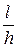по минимальным значениям, при которых разрушений от не будет.

Проверка на жесткость изгибаемых элементов заключается в определении прогиба или относительного прогиба и сравнению его с предельно допустимыми значениями .

Прогиб шарнирно опертых и консольно-изгибаемых элементов определяется по формуле

,

где - прогиб элементов постоянного сечения без учета деформации сдвига;

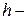наибольшая высота сечения; 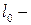расчетный пролет элемента;

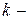коэффициент, учитывающий переменность высоты сечения элемента (табл. СНиП II-25-80);

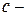коэффициент, учитывающий влияние деформаций сдвига на прогиб (табл. СНиП). Предельные прогибы изгибаемых элементов даны в СНиП.

Дата добавления: 2014-01-05