Понятие определенного интеграла

Определенный интеграл

Пусть на отрезке [а, b] задана неотрицательная функция у = f(x). Требуется найти площадь S криволинейной трапеции, ограниченной кривой у = f(x), прямыми х = а, х = b и осью абсцисс y = 0 (рисунок 4.1).

Для этого введем в рассмотрение ломаную линию, которая расположена достаточно близко к кривой у = f(x) на [а, b] (рисунок 4.2). Фигура под ломаной состоит из трапеций. Ее площадь S_лом равна сумме площадей этих трапеций, и ее можно вычислить по формулам, известным из школьного курса планиметрии. Поскольку ломаная выбрана достаточно близко к кривой у = f(x), справедливо приближенное равенство S» S_лом. Оно тем точнее, чем ближе расположена ломаная к исходной кривой. Искомую площадь S можно рассматривать, как предел площади S_лом при неограниченном приближении ломаной к заданной кривой.

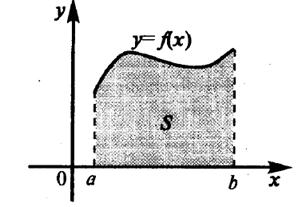
Рисунок 4.1 – Площадь криволинейной трапеции

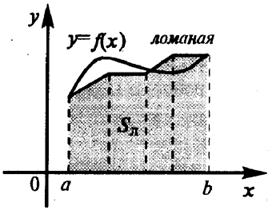
Рисунок 4.2 – Площадь под ломаной

Рассмотрим более подробно процедуру выбора ломаной. Разобьем отрезок [а, b], на котором определена некоторая функция у = f(x), на n отрезков точками х₀, x₁, x₂, …x_n: a = x₀ < x₁ < x₂ < …< x_n = b. На каждом отрезке [x_i-1; x_i] (Dx_i = x_i-1 - x_i) выберем некоторую точку x_i («кси»). Сумма вида 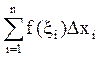называется интегральной суммой для
функции у = f(x) на отрезке [а, b].

Для неотрицательной функции у = f(x) каждое слагаемое в этой сумме равно площади S_i прямоугольника со сторонами f(x_i) и Dx_i (это площадь под прямой у = f(x_i) на отрезке [x_i-1; x_i]) (рисунок 4.3). Поэтому вся интегральная сумма равна площади 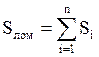(это площадь под ломаной, образованной на каждом из отрезков [x_i-1; x_i] прямой у = f(x_i), параллельной оси абсцисс).

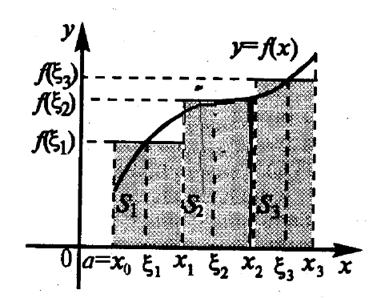
Рисунок 4.3 – Интегральная сумма

Наибольшую из длин отрезков [x_i-1; x_i] обозначим 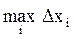. Отметим, что при стремлении 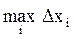к нулю ломаная неограниченно приближается к исходной кривой, и площадь под ломаной переходит в площадь криволинейной трапеции.

Пусть предел интегральной суммы при стремлении 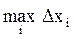к нулю существует, конечен и не зависит от способа выбора точек x_i и x_i. Тогда этот предел называется определенным интегралом от функции у = f(x) на [а, b] и обозначается 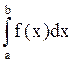, а сама функция называется интегрируемой на отрезке [а, b], т.е. .

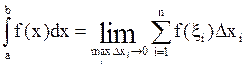При этом число а называется нижним пределом определенного интеграла, число b - его верхним пределом; функция f(x) — подынтегральной функцией, выражение f(x)dx - подынтегральным выражением, а задача о нахождении 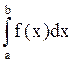- интегрированием функции f(x) на отрезке [а, b].

Подчеркнем, что определенный и неопределенный интегралы существенно различаются между собой. Если неопределенный интеграл представляет семейство функций, то определенный - есть определенное число.

Отметим, что если подынтегральная функция представляет собой константу, т.е. f(x) = C, то интегральная сумма примет вид 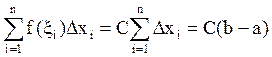, т.е. будет представлять собой константу. Поэтому предел этой суммы тоже будет равен этой константе .

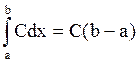На рисунке 4.4 видно, что эта величина равна площади прямоугольника под графиком функции f(x) = C.

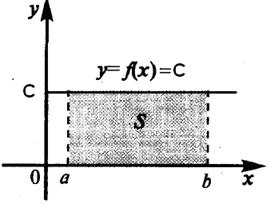
Рисунок 4.4 – Интеграл от константы равен площади прямоугольника

Во введенном определении определенного интеграла 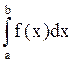предполагается, что а < b. По определению положим .

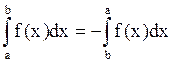Это позволят считать несущественным, какой из пределов интегрирования больше: верхний или нижний.

Если пределы интегрирования равны друг другу (а = b), то из 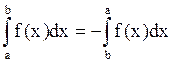получим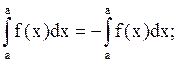

.

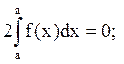
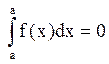Теорема (достаточное условие существования определенного интеграла (интегрируемости функции)). Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.

Дата добавления: 2014-01-05