Геометрический и экономический смысл определенного интеграла

Из определения следует, что для неотрицательной функции f(x) определенный интеграл 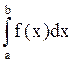равен площади криволинейной трапеции, ограниченной кривой у = f(x), прямыми х = а, х = b и осью абсцисс y = 0 (рисунок 4.1).

Если функция – f(x) неположительна, то определенный интеграл 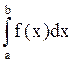равен площади соответствующей криволинейной трапеции, взятой со знаком минус (рисунок 4.7).

Рисунок 4.7 – Геометрический смысл определенного интеграла для неположительной функции

Для произвольной непрерывной функции f(x) определенный интеграл 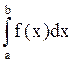равен сумме площадей криволинейных трапеций, лежащих под графиком функции f(x) и выше оси абсцисс, за вычетом суммы площадей криволинейных трапеций, лежащих над графиком функции f(x) и ниже оси абсцисс (рисунок 4.8).

Рисунок 4.8 – Геометрический смысл определенного интеграла для произвольной непрерывной функции f(x) (знаком «плюс» помечена площадь, которую прибавляют, а «минусом» - та, которую вычитают).

При вычислении на практике площадей криволинейных фигур часто используется следующая формула: , где S – площадь фигуры, заключенной между кривыми y = f₁(x) и y = f₂(x) на отрезке [а, b], а f₁(x) и f₂(x) - непрерывные функции, заданные на этом отрезке, такие, что f₁(x) ≥ f₂(x) (см. рисунки 4.9, 4.10, 4.11).

При изучении экономического смысла производной было выяснено, что производная выступает как скорость изменения некоторого экономического объекта или процесса во времени или относительного другого исследуемого фактора. Чтобы установить экономический смысл определенного интеграла, необходимо саму эту скорость рассмотреть в виде функции от времени или другого фактора. Тогда, так как определенный интеграл представляет собой изменение первообразной, мы получим, что в экономике он представляет собой оценку изменения этого объекта (процесса) за определенный период времени (или при определенном изменении другого фактора).

Например, если функция q = q(t) описывает производительность труда в зависимости от времени, то определенный интеграл от этой функции 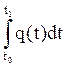представляет собой объем выпущенной продукции Q за промежуток времени от t₀ до t₁.

Методы вычисления определенных интегралов основаны на рассмотренных ранее методах интегрирования (доказательств проводить не будем).

При нахождении неопределенного интеграла мы пользовались методом замены переменной, основанным на формуле: ò f(x)dx =
= ò f(j(t)) j`(t) dt, где x = j(t) - функция, дифференцируемая на рассматриваемом промежутке. Для определенного интеграла формула замены переменной примет вид , гдеи для всех .

Пример 1. Найти

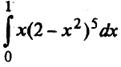
Пусть t = 2 – x². Тогда dt = -2xdx и xdx = - ½ dt.

При х = 0 t = 2 – 0² = 2. При х = 1 t = 2 – 1² = 1. Тогда

Пример 2. Найти

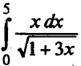
Пример 3. Найти

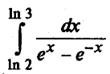
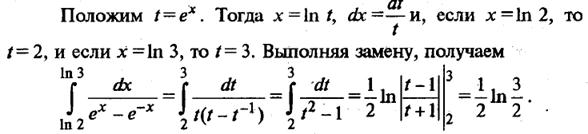
Формула интегрирования по частям для определенного интеграла примет вид: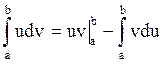, где .

Пример 1. Найти

Пусть u = ln (1 + x), dv = dx. Тогда

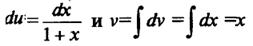
Пример 2. Найти

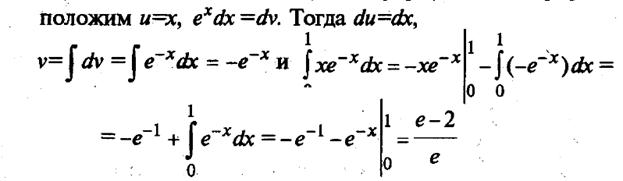
Дата добавления: 2014-01-05