
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнения Рейнольдса для осредненного турбулентного движения
|
|
|
|
Как уже отмечалось, сложность турбулентного движения делает невозможным строгое математическое рассмотрение течений при заданных граничных условиях. Одной из возможных альтернатив является переход от истинной картины, детали которой нам неизвестны, к рассмотрению осредненного турбулентного течения, т.е., по существу, замена принципиально неустановившегося движения квазистационарным. Переход, предложенный в свое время О.Рейнольдсом, состоит в том, что в уравнениях движения вязкой жидкости и уравнении неразрывности истинные значения параметров заменяются их осредненными значениями.
 ,
,  ,
, 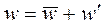 ,
,
где u,v,w, - действительные (актуальные) мгновенные скорости потока в данной точке, 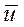 ,
,  ,
,  - осредненные во времени скорости,
- осредненные во времени скорости, 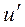 ,
, 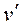 ,
, 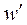 - отклонения действительных скоростей от осредненных, или пульсации скоростей. Представление об операции осреднения изложено ранее, здесь отметим лишь некоторые свойства этого преобразования.
- отклонения действительных скоростей от осредненных, или пульсации скоростей. Представление об операции осреднения изложено ранее, здесь отметим лишь некоторые свойства этого преобразования.
Если в результате осреднения какой-либо характеризующей течение функции, проведенного в данной точке в разные моменты времени, получаются те же значения осредненной функции, то такое осредненное течение называется стационарным, а само турбулентное движение – квазистационарным.
 ,
, 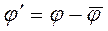 ,
, 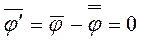
В дальнейшем будем иметь дело исключительно с квазистационарными турбулентными движениями, и осредненное значение  будет функцией только координат. При этом, если
будет функцией только координат. При этом, если 
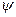 является еще одной пульсирующей функцией времени и координат, то, очевидно, что
является еще одной пульсирующей функцией времени и координат, то, очевидно, что 
 . Из определения операции осреднения следует также, что среднее значение производной от некоторойфункции по координате равно производной от среднего значения этой функции:
. Из определения операции осреднения следует также, что среднее значение производной от некоторойфункции по координате равно производной от среднего значения этой функции: 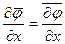 . Этим свойством обладает и производная по времени:
. Этим свойством обладает и производная по времени: 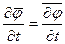 .
.
Используя указанные свойства операции осреднения можно получить дифференциальные уравнения осредненного движения несжимаемой вязкойжидкости. Возьмем для примера уравнение движения Навье-Стокса лишь для одной проекции скорости (на ось х) и уравнение несжимаемости:
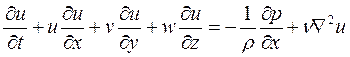 ,
,  ,
,
и пользуясь последним из них, перепишем первое в виде:
 .
.
Произведем над обеими частями этого уравнения операцию осреднения, учитывая ее свойства и то, что ρ=const, ν=const, в результате получим:
 .
.
Рассмотрим отдельно входящие в уравнение средние значения от произведений проекций скоростей:
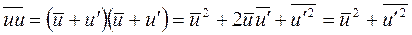

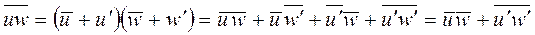
После произведенных преобразований уравнение осредненного движения может быть переписано в форме:
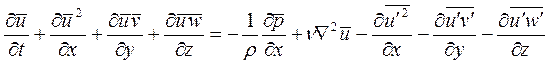
Заметим, что осреднение уравнения неразрывности дает:

С использованием этого осредненного уравнения неразрывности уравнение осредненного движения можно преобразовать к виду:

Проделав те же операции с двумя другими уравнениями Навье-Стокса для проекций скорости можно получить еще два дифференциальных уравнения осредненного движения. Совместно с осредненным уравнением неразрывности они образуют систему уравнений Рейнольдса для осредненных скоростей и давления в турбулентных течениях.
Сопоставив эти уравнения с общими уравнениями в напряжениях:
 ,
,
можем представить себе правые части системы осредненных уравнений как результат подстановки на место  ,
,  , и т.д. суммы вязких напряжений, определенных обобщенным законом Ньютона и дополнительных турбулентных напряжений, возникающих за счет наличия в потоке пульсаций:
, и т.д. суммы вязких напряжений, определенных обобщенным законом Ньютона и дополнительных турбулентных напряжений, возникающих за счет наличия в потоке пульсаций:
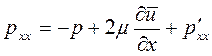 ,
, 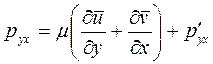 и т.д.,
и т.д.,
причем эти дополнительные турбулентные напряжения, получившие название Рейнольдсовых, образуют, так же как вязкие напряжения, симметричный тензор второго ранга:
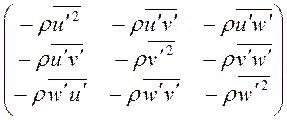
Таким образом, в осредненном турбулентном потоке к обычным вязким напряжениям добавляются напряжения, зависящие от пульсаций скорости. Физически это объясняется тем, что между разными участками турбулентного потока происходит обмен количеством движения, обусловленный перемешиванием частиц. Перенос количества движения вызывает дополнительное торможение либо ускорение отдельных масс жидкости, т.е. приводит к возникновению турбулентных напряжений.
Поскольку исходная система уравнений Навье-Стокса являлась замкнутой (четыре уравнения и четыре неизвестных - u, v, w, p) то появление дополнительных членов в уравнениях Рейнольдса приводит к тому, что она превращается в незамкнутую. Возникает новая проблема «замыкания системы уравнений Рейнольдса», т.е необходимы дополнительные предположения о связи турбулентных напряжений с другими характеристиками потока.
Представим, что турбулентные напряжения подчинены закону, аналогичному обобщенному закону Ньютона, тогда, например, в случае плоского прямолинейного и параллельного оси х осредненного течения со скоростью  , являющейся функцией только от y получим:
, являющейся функцией только от y получим:
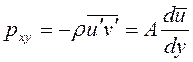
Величину А можно рассматривать как коэффициент эффективной турбулентной вязкости, обусловленной не микропереносом молекул, а возникающим между соседними слоями осредненного движения макропереносом (пульсационным) количества движения конечных объемов жидкости. Если в частном случае движения в плоской трубе предположить, что А – постоянная величина, рассчитать и измерить сопротивление трубы, аналогично тому как это было сделано при ламинарном режиме течения, то полученные величины А окажутся в десятки тысяч раз превосходящими величину коэффициента молекулярной динамической вязкости μ. Вместе с тем измерения показывают, что величина А, в отличие от μ, не является постоянной, зависящей от рода жидкости или ее турбулентного течения. Величина А сильно изменяется поперек сечения трубы от малых значений у стенки трубы до некоторого максимума примерно на расстоянии полурадиуса от стенки и затем вновь убывает до оси трубы.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 3301; Нарушение авторских прав?; Мы поможем в написании вашей работы!