Двоичные числа

Представление информации в ЭВМ.

ЭВМ оперирует с данными трёх основных типов: числами, строками символов и логическими значениями.

Основной формой представления числовых значений в ЭВМ являются двоичные числа. Двоичные числа – это значения представленные в двоичной системе счисления. Числовые значения могут быть двух типов: целые и действительные и для их изображения в ЭВМ используют две формы: с фиксированной запятой (точкой) и с плавающей запятой (точкой).

Представление числа с фиксированной запятой имеет следующий формат (структуру):

(1.5)

Разряд с номером «n» является знаком числа: знак «+» кодируется цифрой 0, а знак «-» - цифрой 1. Разряды от 0 до n-1 являются цифровыми. Запятая фиксируется в определённом месте относительно разрядов числа. Обычно она находится или перед старшим разрядом или после младшего. Формат числа с фиксированной запятой после младшего разряда служит для изображения целых чисел N. Число разрядов n определяет диапазон значений, которые могут быть представлены в этом формате: NÎ[-(2ⁿ-1),+(2ⁿ-1)].

Увеличение количества цифровых разрядов n на единицу расширяет диапазон значений в два раза.

Выполнение операций над целыми числами, изображаемыми словами фиксированной длины, имеет следующие особенности. Операции сложения и вычитания определены только в том случае, если результат может быть представлен в n цифровых разрядах, т. е. если результат |C|<2ⁿ. В противном случае говорят, что результат переполняет размерную сетку ЭВМ. Если |C|³2ⁿ в процессоре формируется признак переполнения, используемый для прекращения вычислений.

Формат числа с запятой, фиксированной перед старшими разрядом, используется для представления действительных чисел, принадлежащих отрезку [-(1-2^-n),+(1-2^-n)] и изменяются с шагом 2^-n. В отличие от целых, они представляются приближённо с погрешностью D=2^-(n+1). Отсюда следует, что количество цифровых разрядов определяет точность представления значений числами с фиксированной запятой. С увеличением n на один дополнительный разряд погрешность D уменьшается в два раза.

Выполнение операций над действительными числами в форме с фиксированной запятой имеет следующие особенности. Операции сложения и вычитания определены в том случае, если результат может быть представлен в форме с фиксированной запятой, т.е. если результат |C|<1. В противном случае фиксируется переполнение. Деление А/B возможно, если B¹0 и |A|<|B|.

В современных ЭВМ для представления действительных чисел широкое распространение получил другой способ – представление чисел с плавающей запятой. При этом число представляется в виде:

Z=±Md^±P (1.6)

где d – основание чисел с плавающей запятой.

P – целое число, называемое порядком числа Z;

M – мантисса числа Z.

Как видно из (1.6) число представляет собой произведение мантиссы и экспоненты по основанию d, поэтому такое представление называют также экспоненциальным.

Обычно d=2^r, r=1,2,… В качестве основания d чаще всего используется значение 2 или 16. Мантисса числа с плавающей запятой всегда меньше единицы, и если выполняется условие:

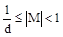, (1.7)

то такое число называется нормализованным. В противном случае число называется ненормализованным.

Число с плавающей запятой имеет следующий формат:

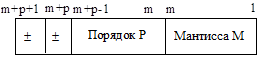
(1.8)

Разряд m+p+1 слова представляет знак числа, который одновременно является знаком мантиссы. Мантисса М представляется m – разрядным числом с фиксированной запятой. Знак порядка кодируется «m+p» - ым разрядом слова. Порядок Р является целым числом и занимает р разрядов с m по m+p+1. У нормализованных чисел r старших разрядов мантиссы не равны нулю.

В ЭВМ знак порядка и порядок представляются одним (р+1) – разрядным целым значением Х, называемым характеристикой числа с плавающей запятой, которая связана с порядком соотношением:

X=2^P+P, (1.9)

С учётом этого порядок определяется по значению характеристики Х следующим образом:

P=2^P-X, (1.10)

где 0£X£2^P+1-1

Как следует из (1.9) и (1.10), значение характеристики 0,1,2,…,2^P используются для представления порядков –2^P,-(2^P-1),-(2^P-2),…,0 соответственно, а значения характеристики 2^P+1, 2^P+2,…,2^P+(2^P-1) – значения для представления порядков 0,1,2,…,2^P–1. При этом нулевое значение старшего разряда характеристики соответствует знаку порядку минус, а единичное значение – знаку плюс. Таким образом, характеристика – это дополнительный код порядка с инверсным представлением знака. Использование характеристики несколько упрощает алгоритм операций над числами с плавающей запятой.

Учитывая, что 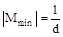и , и 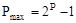, получим, что нормализованные числа с плавающей запятой обеспечивают представление значений в диапазоне

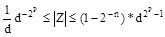(1.11)

с предельной относительной погрешностью

(1.12)

так как 2^-m<<1, выражение (1.11) преобразуется к виду

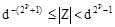, (1.13)

или переходя к десятичному основанию,

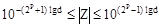(1.14)

За счёт ненормализованных чисел диапазон значений Z расширяется слева на . В этой области значения представляются с предельной относительной погрешностью, лежащий в интервале 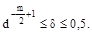Из (1.13) и (1.14) видно, что диапазон определяется величиной основания и порядком, а точность представления чисел количеством разрядов мантисс. Увеличение основания d приводит к существенному расширению диапазона значений, а погрешность при этом увеличивается незначительно. По этой причине в ЭВМ общего назначения, к которым принадлежат ЕС ЭВМ, IBM 360/370, использовалось основание 16.

Из–за ограниченности числа разрядов мантиссы и порядка при выполнении операций над числами с плавающей запятой могут возникать следующие особые случаи.

1. Потеря значимости имеет место при выполнении операций сложения и вычитания, когда при равных порядках модули мантисс равны с точностью до m старших разрядов. В этом случае выполнение операции приводит к числу с нулевой мантиссой и ненулевым порядком, т.е. к числу без значащих цифр. Полученное значение рассматривается как машинный нуль, который представляется словом с нулевыми значениями во всех разрядах.

2. Исчезновение порядка происходит, когда порядок результата должен иметь значение, меньшее –2^P – максимального по модулю отрицательного порядка. В таком случае результат приходиться представлять машинным нулём.

3. Переполнение порядка возникает, когда порядок результата должен иметь значение, превосходящее максимально возможное (2^Р-1). Такое значение не может быть представлено в формате (1.8), поэтому результат операции считается неопределённым, что отличается выработкой признака переполнения.

4. Деление на нуль, которое невозможно, что отличается выработкой признака переполнения.

В современных ЭВМ используются целые числа и числа с плавающей запятой. Целые числа представляются в формате с фиксированной запятой (1.5), расположенной после младшего разряда. Используется представление целых чисел со знаком и без знака. Для примера рассмотрим представление целых чисел в персональных ЭВМ IBM PC.

Для представления действительных чисел с различной точностью используются несколько форматов чисел с плавающей запятой. В персональных ЭВМ IBM PC используются следующие форматы:

Дата добавления: 2014-01-05