Порядок синтеза комбинационных схем

1. Формулировка задания на проектирование комбинационной схемы.

2. Построение таблиц истинности.

3. Получение совершенных нормальных форм (СНФ): совершенной дизъюнктивной нормальной формы (СДНФ) и совершенной конъюнктивной нормальной формы (СКНФ).

4. Получение минимальных нормальных форм: минимальной нормальной дизъюнктивной формы (МДНФ) и минимальной конъюнктивной нормальной формы (МКНФ).

5. Преобразование минимальных нормальных выражений к форме, удобной для реализации с учётом характеристик элементной базы.

В случае необходимости следует:

а) учесть нагрузочную способность;

б) получить скобочную форму, учитывающую ограничения на число входов;

в) получить выражения, свободные от логических состязаний;

г) получить выражения в базисе выбранных логических элементов, например, преобразовать МДНФ или МКНФ в штрих Шеффера или стрелку Пирса, при использовании элементов «И-НЕ», «ИЛИ-НЕ»;

д) система функций должна реализовываться совместно.

2.9.2 Элементы «И», «ИЛИ», «НЕ».

Элемент «И» Элемент «ИЛИ» Элемент «НЕ»

&

Функции «И», «ИЛИ», «НЕ» образуют расширенный булевский базис, поэтому выражения для МДНФ или МКНФ могут использоваться сразу для построения схем. В случае отсутствия элементов с нужным числом входов, может потребоваться преобразование МДНФ или МКНФ к скобочному виду.

2.9.3 Элементы «И-НЕ», «ИЛИ-НЕ».

Элемент «И-НЕ» Элемент «ИЛИ-НЕ»

&

a a F= a↓ b

F=a/b

b b

Запишем основные соотношения для штриха Шеффера и стрелки Пирса:

__ _ _

a / b = a b = a + b;

___ _ _

a↓ b = a v b = a b

Штрих Шеффера и стрелка Пирса функционально полны, поскольку:

___ _ _

a b = a / b = a ↓ b;

_ _ ___

a + b = a / b = a ↓ b.

_ __

a = a a = a / a.

&

_

a

a

_ __

a = a 1 = a / 1

&

a _

+E a

_ ___

a = a + a = a ↓ a

_

a

a

_ ____

a = a + 0 = a ↓ 0

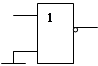a _

a

Штрих Шеффера и стрелка Пирса не являются ассоциативными операциями, то есть:

a / (b / c) 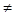a / b / c 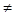(a / b) /c;

a ↓ (b ↓ c) 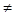a ↓ b ↓ c 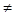(a ↓ b) ↓ c.

При реализации функций на элементах «И-НЕ», «ИЛИ-НЕ» после получения минимальных форм МДНФ и МКНФ, их необходимо представить в базисе «штрих Шеффера» и «стрелка Пирса».

Дата добавления: 2014-01-05