Определение абстрактного автомата

Синтез абстрактных автоматов.

Абстрактный автомат задаётся множеством из шести элементов: S={ X, Y, A, f, g, a⁽⁰⁾} где:

X={x₁,x₂,…,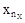} – множество входных сигналов (входной алфавит);

Y={y₁,y₂,…,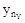} – множество выходных сигналов (выходной алфавит);

А={a₁,a₂,…, 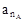} – множество состояний (алфавит состояний);

f – функция переходов автомата;

g – функция выходов автомата;

a⁽⁰⁾ – начальное состояние автомата.

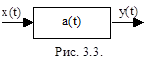Абстрактный автомат (рис.3.3.) имеет один входной и один выходной канал. В каждый момент дискретного автоматного времени t=0,1,2,… автомат находится в определённом состоянии а(t) из множества А состояний автомата, причём в начальный момент t=0 он находится всегда в начальном состоянии a(t₀)=a⁽⁰⁾. Будем считать, что a⁽⁰⁾=a₁. В момент t, будучи в состоянии a(t)ÎA, автомат способен воспринять на входном канале сигнал x(t)ÎX и выдать на выходном канале сигнал y(t)ÎY

y(t)=g(a(t),x(t)),

переходя в состояние а(t+1)

а(t+1)=f(a(t), x(t)).

Другими словами, если на вход автомата, установленного в начальное состояние а₁, подавать буква за буквой некоторую последовательность букв входного алфавита – входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита – выходное слово. Таким образом, абстрактный автомат осуществляет словарное преобразование входных слов в выходные.

Автомат называется конечным, если конечные алфавиты A, X, Y. В дальнейшем будем рассматривать только конечные автоматы и термин «конечные» будем опускать. Автомат называется полностью определённым (полный автомат), если функции выходов g и переходов f определены на множестве всех пар вида <a_m,x_j>, где a_mÎA, x_jÎX. У частичного автомата функции g и f определены не для всех пар <a_m,x_j>.

На практике наибольшее распространение получили автомат Мили и Мура, которые отличаются способом формирования выходного сигнала g(t).

Закон функционирования автомата Мили задаётся уравнениями

а(t+1)=f(a(t), x(t)); t=0,1,2,…

y(t)=g(a(t), x(t)),

а закон функционирования автомата Мура задаётся уравнениями

а(t+1)=f(a(t), x(t)); t=0,1,2,…

y(t)=g(a(t)).

В автомате Мура выходной сигнал формируется в состоянии a(t), а в автомате Мили на переходе из a(t) в a(t+1).

Два автомата с одинаковыми входными и выходными алфавитами называются эквивалентными, если после установления их в начальные состояния их реакции на любые входные слова совпадают, при этом временной сдвиг при формировании выходных последовательностей не учитывается, важно их совпадение.

Для любого автомата Мили существует эквивалентный ему автомат Мура, и наоборот. Выходной сигнал автомата Мура задержан на такт относительно выходного сигнала эквивалентного ему автомата Мили.

Дата добавления: 2014-01-05