Преобразование Лапласа

Математический аппарат описания сигналов и линейных систем

Во временной области:

Сигналы (а/g) описываются функциями времени. Линейные системы (а/g) описываются:

а) характеристиками. Характеристика – реакция системы на тестовый сигнал. Т.о. характеристика представляет собой сигнал, описываемый функцией времени.

б) соотношением вход-выход, представляет собой линейное уравнение, описывающее связь между входными и выходными сигналами как функциями времени.

Тип функции времени зависит от типа сигнала:

непрерывная функция x(t) описывает аналоговый сигнал,

последовательность (или решетчатая функция) x(nT) – дискретный сигнал.

Помимо временной сигналы и линейные системы можно описывать и в других областях(областях иных независимых переменных),при этом соответствующие функции времени преобразуются в функции других переменных по определенным правилам.

В ЦОС наиболее распространены обозначения сигналов:

1)В области комплексных переменных:

р - область для непрерывных функций x(t);

z – область для последовательностей x(nT).

2)В частотной области.

2. Математическое описание аналоговых сигналов и линейных систем.

Пусть x=x(t); x(t)_t<0=0, тогда возможно представление сигнала в области комплексных переменных(на комплексной р- области), как изображение Лапласа.

Прямое: 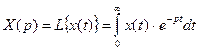(1)

Обратное: 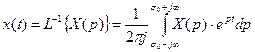(2),

где L{} – оператор преобразования Лапласа; р – оператор Лапласа; 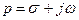, σ₀ – абсцисса абсолютной сходимости (1)

x(t) – оригинал –вещественная или комплексная функция, кусочно-непрерывная, однозначная, имеющая экспоненциальный порядок 0(е^λt) и ограниченно возрастающая 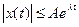, А, λ≠∞.

L{} справедливо только в области абсолютной сходимости интеграла(1): 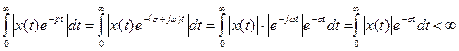(3),

определяемой σ₀. Если сходится (3), то сходится и (2), но не всегда наоборот.

Дата добавления: 2014-01-05