Случайные погрешности

Мы убедились, что результат измерения случайная величина. В связи с этим при проведении любых измерений наряду с получением числа, выраженного в определенных единицах (результата измерений), необходимо определить степень достоверности результата измерения.

Количественно оценить степень достоверности результата измерения – означает получение количественной меры близости между случайным результатом измерения и неизвестным (но не случайным) истинным значением измеряемой величины.

Из теории вероятностей известно, что случайные величины исчерпывающе описываются законами распределения. Обычно дифференциальный закон распределения (плотность распределения вероятностей) .

Одним из наиболее распространенных законов распределения случайной погрешности является нормальный закон распределения

(3.7)

где .

Из 3.7 видно, что нормальный закон распределения целиком определяется двумя параметрам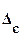и - и 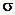. В теории вероятности принято называть математическим ожиданием случайной величины 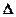, а в метрологии – систематической погрешностью (когда 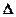- абсолютная погрешность). В теории вероятностей 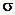принято называть дисперсией случайной величины 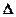, а в метрологии эта величина является мерой

Величины и 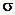имеют размерность погрешности 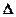и поэтому удобны в качестве ее характеристики.

Вид нормального закона распределения представлен на рис. 3.2

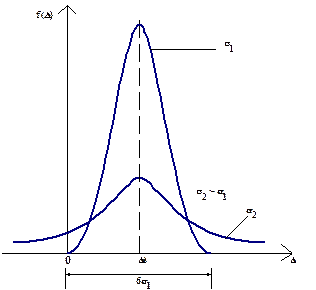
Рис. 3.2 – нормальный закон распределения погрешностей

Из 3.7 следует, что лежит на оси симметрии кривой , т.е. систематическую погрешность можно рассматривать как среднее значение погрешностей, которые получаются при многократных измерениях одного и того же размера физической величины. Поэтому систематическую погрешность считают величиной постоянной. Из 3.7 так же следует, что чем больше 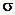, тем кривая более полога и имеет меньший максимум, т.е чем больше 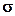, тем более вероятны значительные отклонения погрешностей от их среднего значения.

При нормальном законе распределения погрешностей, вероятность того что погрешность отдельного измерения превысит по абсолютной величине 3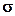, составляет 0,003 (0,3%). Такой вероятностью на практике пренебрегают и называют величину 3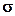максимально возможной погрешностью («закон трёх сигм»).

Если величине известна и исключена из результата измерения, то это эквивалентно переносу начала координат на рис.3.2 в точку. В этом случае математическое ожидание погрешности 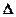, составляющей которой, теперь является, только случайная составляющая , будет равно нулю (рис 3.2 преобразуется в рис 3.3)

Рис.3.3. – нормальный закон распределения погрешностей при = 0.

Исключить случайную погрешность из результата однократного измерения нельзя, так как неизвестно, какое конкретное значение примет . Однако можно существенно уменьшить влияние на результат измерения, проводя многократное измерение одного и того же размера физической величины и усредняя их результаты. Иными словами, для исключения случайной погрешности из результата измерения необходимо определить его математическое ожидание, которое и будет истинным значением измеряемой величины .

В этом случае с учётом что плотность распределения результатов однократных измерений будет подчиняться также нормальному закону:

,

где 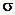- дисперсия результатов однократных измерений равная дисперсии погрешности.

Дата добавления: 2014-01-05