Аппроксимация характеристик нелинейных элементов

Для того чтобы была возможность аналитически рассчитывать цепи с нелинейными элементами, необходимо иметь математические выражения для характеристик элементов. Сами эти характеристики обычно являются экспериментальными, т.е. полученными в результате измерений соответствующих элементов, а затем приводятся как справочные (типовые) данные. Процедуру математического описания некоторой заданной функции в математике называют аппроксимацией этой функции. Существует целый ряд типов аппроксимации: по выбранным точкам, по Тейлору, по Чебышеву и др. В конечном итоге необходимо получить математическое уравнение, которое с какими-то заданными требованиями удовлетворяло исходной, аппроксимирующей функции. Для этого применяют полиномы: степенные, экспоненциальные и тригонометрические.

Рассмотрим простейший способ: метод выбранных точек или узлов интерполяции степенным полиномом.

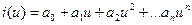
Необходимо определить коэффициенты полинома. Для этого выбирается (n+1) точек на заданной функции и составляется система уравнений:

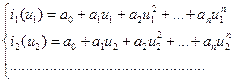
Из этой системы находятся коэффициенты а₀, а₁, а₂, …, а_n.

В выбранных точках аппроксимирующая функция будет совпадать с исходной, в других точках – отличаться (сильно или нет – зависит от степенного полинома).

Можно использовать экспоненциальный полином:

Второй метод: метод аппроксимации по Тейлору. В этом случае выбирается одно точка, где будет совпадение исходной функции с аппроксимирующей, но дополнительно ставится условие, чтобы в этой точке совпадали еще и производные.

Аппроксимация по Батерворту: выбирается простейший полином:

В этом случае можно определить максимальное отклонение ε.

Аппроксимация по Чебышеву является степенной, там устанавливается совпадение в нескольких точках и минимизируется максимальное отклонение аппроксимирующей функции от исходной.

Чебышев установил, что должно выполняться:

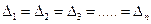
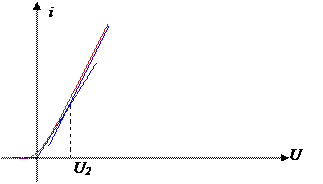
В инженерной практике используется еще так называемая кусочно-линейная аппроксимация – это описание заданной кривой отрезками прямых линий.

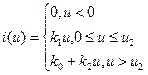
Дата добавления: 2014-01-05