Вводные замечания

ИССЛЕДОВАНИЕ НЕУСТАНОВИВШИХСЯ ПРОЦЕССОВ, ВЫЗВАННЫХ ПУСКОМ ИЛИ ОСТАНОВКОЙ СКВАЖИНЫ В ПРОСТЕЙШИХ УСЛОВИЯХ УПРУГО-ВОДОНАПОРНОГО РЕЖИМА

(В.Н.Щелкачев. Разработка месторождений на упруго водонапорном режиме)

Как было установлено в главе I, для упруго-водонапорного режима характерно, что разрабатываемая залежь нефти гидравлически связана с окружающей ее пластовой водонапорной системой, причем запас жидкости в пласте может пополняться за счет ее притока из области питания. Данная глава посвящена анализу проявлений упруго-водонапорного режима в сравнительно простейших и весьма важных для практики условиях. Именно, анализу подвергнуты неустановившиеся процессы перераспределения пластового давления при плоско-радиальном движении жидкости в пласте, вызванные пуском или остановкой одной эксплуатационной или нагнетательной скважины. В одной из задач исследуется еще и неустановившийся процесс изменения дебита возмущающей скважины.

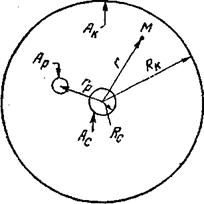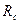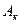Рис. 5. Схема пласта с круговой внешней границей и с расположенной в центре возмущающей скважиной . - возмущающая эксплуатационная (или нагнетательная) скважина радиуса ; - круговой контур питания радиуса 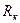; 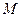– любая точка в пласте на расстоянии r от центра скважины; 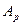- реагирующая (наблюдательная бездействующая) скважина, расположенная на расстоянии 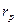от центра возмущающей скважины.

Установившееся распределение пластового давления при плоско-радиальном движении и при условиях, оговоренных в § 5 главы I, обладает закономерностями, хорошо известными из подземной гидравлики и вытекающими из анализа формул Дюпюи (см. формулы (II.14) и (II.17) данной главы). Для удобства сопоставления с упомянутым установившимся движением жидкости будем рассматривать в данной главе неустановившиеся процессы, вызванные пуском или остановкой скважины в центре конечного пласта с круговым контуром питания, вдоль которого все время удерживается постоянное давление, равное начальному пластовому давлению.

В данной главе мы попутно выясним влияние размеров и формы внешней границы пласта и подметим также особенности в интересующих нас процессах перераспределения пластового давления, которые позволят перейти от модели конечного пласта к модели бесконечного пласта. Последнее очень важно потому, что соответствующие формулы для бесконечного пласта гораздо проще формул для конечного пласта. Поэтому читатель может не обращать особого внимания на упоминаемые в данной главе (и приведенные в главе XIII) довольно громоздкие формулы, относящиеся к конечному круговому пласту. В главе IV читатель убедится в том, что очень часто оказывается возможным использовать для расчетов сравнительно простые, формулы, выведенные для модели бесконечного пласта 1.

Рассмотрим постановку трех основных задач, которые нам придется всесторонне исследовать в данной главе. Для наглядности рассуждений воспользуемся схемой, представленной на рис. 52.

Для удобства чертежа скважины и круговой контур питания на рис. 5 изображены без соблюдения масштаба.

Постановка задачи I. В некоторый момент времени, который принимаем за начальный (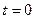; 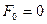), быстро останавливаем эксплуатационную фонтанную возмущающую скважину. Считаем, что после остановки приток жидкости из пласта в скважину сразу прекращается, как будто бы скважина мгновенно закрывается на забое. Предположим, что перед остановкой скважина длительно работала с практически установившимся дебитом 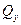и установившимся давлением на забое 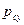. Перед остановкой установившееся давление в пласте (вокруг скважины) распределялось по логарифмическому закону. После остановки возмущающей скважины начинается процесс восстановления пластового давления. Необходимо исследовать все особенности этого процесса, считая, что вдоль кругового контура питания все время удерживается постоянное давление 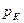, равное начальному статическому пластовому давлению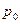, т.е.

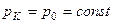(II.1)

Постановка задачи II. Пусть давление во всем пласте — внутри кругового контура питания 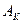— одинаково и равно 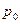. В некоторый момент времени, принимаемый за начальный (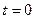, 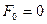), вводим в эксплуатацию возмущающую скважину 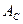с постоянным дебитом (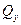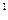. После пуска возмущающей скважины начнется процесс падения пластового давления. Необходимо исследовать все особенности этого процесса, считая опять, что на контуре питания 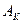все время удерживается постоянное давление 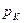равное начальному статическому пластовому давлению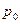. В главе V, используя метод суперпозиции, будет доказано, что распределение давления в пласте после остановки скважины (задача I) можно определить, зная распределение давления после ее пуска (задача II). В данной главе мы пока не будем пользоваться методом суперпозиции.

¹ Кроме того, в тех случаях, когда нельзя воспользоваться моделью бесконечного пласта, часто оказывается возможным использовать простые приближенные формулы (вместо громоздких точных) для конечного кругового пласта (см., например, § 8 главы VII и главу VIII).

² В условиях плоско-параллельного движения будем говорить о центре скважины, о круговой границе пласта и т.п. вместо того, чтобы говорить об оси скважины, о цилиндрической границе пласта и т.д.

Постановка задачи III. Допустим, что перед пуском в эксплуатацию скважины давление во всем пласте было постоянно и равно 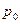. При пуске скважины давление на ее забое было мгновенно снижено до величины 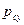, и в дальнейшем оно выдерживается неизменным. Считаем, что на круговом контуре области питания все время сохраняется начальное пластовое давление, т.е. равенство (II. 1) опять справедливо. Требуется определить, как будет перераспределяться давление во всем пласте, и как будет уменьшаться дебит возмущающей скважины после ее пуска.

Постановка данной задачи отличается от постановки задачи II только тем, что здесь предполагается постоянство забойного давления в возмущающей скважине после ее пуска и потому дебит ее оказывается переменным (уменьшающимся). Наоборот, в условии задачи II задавался постоянным дебит пущенной возмущающей скважины, а ее забойное давление с течением времени уменьшалось.

При формулировке задач I и II всюду говорилось об эксплуатационной возмущающей скважине. Однако постановка задачи и результаты ее решения остаются полностью справедливыми и для нагнетательной возмущающей скважины. Единственное различие будет в том, что после пуска нагнетательной скважины придется говорить о повышении, а после ее остановки о понижении пластового давления. Поэтому в дальнейшем мы будем почти всюду рассматривать только эксплуатационные возмущающие скважины, предоставляя читателю перефразировать выводы применительно к нагнетательным скважинам.

Дата добавления: 2014-01-05